二叉树

二叉树的前序遍历

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/binary-tree-preorder-traversal/

问题叙述

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例 1

输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2

输入：root = []
输出：[]

示例 3

输入：root = [1]
输出：[1]

示例 4

输入：root = [1,2]
输出：[1,2]

示例 5

输入：root = [1,null,2]
输出：[1,2]

提示

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶

递归算法很简单，你可以通过迭代算法完成吗？

分析

往左下走到头 无路可走的时候弹栈 往右走一步 继续往左走到头

Code

//递归
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        ArrayList<Integer> list = new ArrayList<>();
        pre(list, root);
        return list;
    }

    void pre(List<Integer> list, TreeNode node) {
        if (node == null) return;
        list.add(node.val);
        pre(list, node.left);
        pre(list, node.right);
    }
}
//迭代
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        ArrayList<Integer> res = new ArrayList<>();
        LinkedList<TreeNode> stack = new LinkedList<>();
        while (!stack.isEmpty() || root != null) {
            while (root != null) {
                res.add(root.val);
                stack.push(root);
                root = root.left;
            }
            TreeNode tmp = stack.poll();
            root = tmp.right;
        }
        return res;

    }
}

二叉树的中序遍历

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/binary-tree-inorder-traversal/

问题叙述

给定一个二叉树的根节点 root ，返回它的 中序 遍历。

示例 1

输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2

输入：root = []
输出：[]

示例 3

输入：root = [1]
输出：[1]

示例 4

输入：root = [1,2]
输出：[2,1]

示例 5

输入：root = [1,null,2]
输出：[1,2]

提示

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶

递归算法很简单，你可以通过迭代算法完成吗？

分析

迭代算法和之前的前序遍历差不多

Code

//递归
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        inorder(root, list);
        return list;
    }

    void inorder(TreeNode root, List<Integer> list) {
        if (root == null) return;
        inorder(root.left, list);
        list.add(root.val);
        inorder(root.right, list);
    }
}


//迭代
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        ArrayList<Integer> res = new ArrayList<>();
        LinkedList<TreeNode> stack = new LinkedList<>();
        while (!stack.isEmpty() || root != null) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.poll();
            res.add(root.val);
            root = root.right;
        }
        return res;
    }
}

二叉树的后序遍历

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/binary-tree-postorder-traversal/

问题叙述

给你一棵二叉树的根节点 root ，返回其节点值的后序遍历 。

示例 1

输入：root = [1,null,2,3]
输出：[3,2,1]

示例 2

输入：root = []
输出：[]

示例 3

输入：root = [1]
输出：[1]

提示

树中节点的数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶

递归算法很简单，你可以通过迭代算法完成吗？

分析

迭代算法几乎和前序遍历一模一样 前序遍历是按照 中左右遍历，那后序遍历我们按照 中右左 再逆序即可

Code

//递归
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        postorder(root, list);
        return list;
    }

    void postorder(TreeNode root, List<Integer> list) {
        if (root == null) return;
        postorder(root.left, list);
        postorder(root.right, list);
        list.add(root.val);
    }
}


//迭代
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        ArrayList<Integer> res = new ArrayList<>();
        LinkedList<TreeNode> stack = new LinkedList<>();
        while (!stack.isEmpty() || root != null) {
            while (root != null) {
                res.add(root.val);
                stack.push(root);
                root = root.right;
            }
            TreeNode tmp = stack.poll();
            root = tmp.left;
        }
        Collections.reverse(res);
        return res;
    }
}

二叉树的层序遍历

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/binary-tree-level-order-traversal/

问题叙述

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1

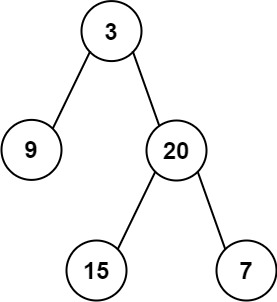
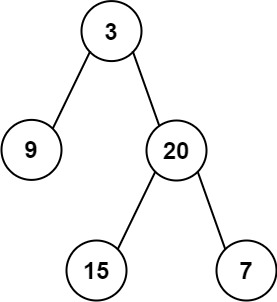
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2

输入：root = [1]
输出：[[1]]

示例 3

输入：root = []
输出：[]

提示

树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000

分析

一层一层模拟
首先先将根节点加入到队列中
将每一层的元素入队后，记录队列中的元素个数(levelCount)
新建一个列表，将该层所有节点出队，每个节点出队的同时，将它的子节点入队
这样能保证每次遍历时，队列中的元素个数是每一层的元素个数
将这个列表添加到结果列表中
往复进行这个操作，直到队为空

Code

//学会层序遍历之后，下面的十道题都可以通杀
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        ArrayList<List<Integer>> res = new ArrayList<>();
        if (root == null) return res;
        LinkedList<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            ArrayList<Integer> list = new ArrayList<>();
            for (int i = 0; i < size; i++) {
                TreeNode tmp = deque.pollFirst();
                list.add(tmp.val);
                if (tmp.left != null) deque.offer(tmp.left);
                if (tmp.right != null) deque.offer(tmp.right);
            }
            res.add(list);
        }
        return res;
    }
}

二叉树的层序遍历II

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/binary-tree-level-order-traversal-ii/

问题叙述

给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

示例 1

输入：root = [3,9,20,null,null,15,7]
输出：[[15,7],[9,20],[3]]

示例 2

输入：root = [1]
输出：[[1]]

示例 3

输入：root = []
输出：[]

提示

树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000

分析

在上题的代码上加一行逆序即可

Code

class Solution {
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        ArrayList<List<Integer>> res = new ArrayList<>();
        if (root == null) return res;
        LinkedList<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            ArrayList<Integer> list = new ArrayList<>();
            for (int i = 0; i < size; i++) {
                TreeNode tmp = deque.pollFirst();
                list.add(tmp.val);
                if (tmp.left != null) deque.offer(tmp.left);
                if (tmp.right != null) deque.offer(tmp.right);
            }
            res.add(list);
        }
        Collections.reverse(res);
        return res;
    }
}

N叉树的层序遍历

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/n-ary-tree-level-order-traversal/

问题叙述

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。
树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

示例 1

输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]

示例 2

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

提示

树的高度不会超过 1000
树的节点总数在 [0, 10^4] 之间

分析

跟层序遍历的区别只有判断子节点是否为空

Code

class Solution {
    public List<List<Integer>> levelOrder(Node root) {
        ArrayList<List<Integer>> res = new ArrayList<>();
        if (root == null) return res;
        LinkedList<Node> deque = new LinkedList<>();
        deque.offer(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            ArrayList<Integer> list = new ArrayList<>();
            for (int i = 0; i < size; i++) {
                Node tmp = deque.pollFirst();
                list.add(tmp.val);
                for (Node child : tmp.children) {
                    if (child != null)
                        deque.offer(child);
                }
            }
            res.add(list);
        }
        return res;
    }
}

二叉树的右视图

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/binary-tree-right-side-view/

问题叙述

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

示例 2

输入: [1,null,3]
输出: [1,3]

示例 3

输入: []
输出: []

提示

二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100

分析

遍历到每层最后一个元素时，将它加入结果集合即可

Code

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        ArrayList<Integer> res = new ArrayList<>();
        if (root == null) return res;
        LinkedList<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            for (int i = 0; i < size; i++) {
                TreeNode tmp = deque.pollFirst();
                if (tmp.left != null) deque.offer(tmp.left);
                if (tmp.right != null) deque.offer(tmp.right);
                if (i == size - 1)
                    res.add(tmp.val);
            }
        }
        return res;
    }
}

二叉树的层平均值

来源：力扣（Leetcode）
链接：https://leetcode.cn/problems/average-of-levels-in-binary-tree/

问题叙述

给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。

示例 1

输入：root = [3,9,20,null,null,15,7]
输出：[3.00000,14.50000,11.00000]
解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。

示例 2

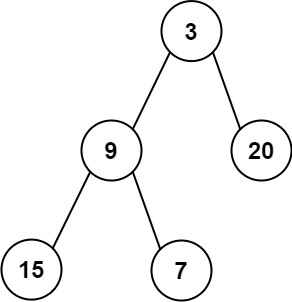
输入：root = [3,9,20,15,7]
输出：[3.00000,14.50000,11.00000]

提示

树中节点数量在 [1, 10^4] 范围内
-2^31 <= Node.val <= 2^31 - 1

分析

一层一层遍历时，用一个变量对当前层的元素求和，再除以size，得到平均值，加入到结果集合中

Code

class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        ArrayList<Double> res = new ArrayList<>();
        LinkedList<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            double sum = 0.0;
            for (int i = 0; i < size; i++) {
                TreeNode tmp = deque.pollFirst();
                sum += tmp.val;
                if (tmp.left != null) deque.offer(tmp.left);
                if (tmp.right != null) deque.offer(tmp.right);
            }
            res.add(sum / size);
        }
        return res;
    }
}

二叉树的最大深度

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/

问题叙述

给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。

示例

给定二叉树 [3,9,20,null,null,15,7]，

3

/
9 20
/
15 7
返回它的最大深度 3 。

分析

每当遍历一层的时候 深度加一即可

Code

class Solution {
    public int maxDepth(TreeNode root) {
        int depth = 0;
        if (root == null) return depth;
        LinkedList<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            depth++;
            for (int i = 0; i < size; i++) {
                TreeNode tmp = deque.pollFirst();
                if (tmp.left != null) deque.offer(tmp.left);
                if (tmp.right != null) deque.offer(tmp.right);
            }
        }
        return depth;
    }
}
//递归
class Solution {
    public int maxDepth(TreeNode root) {
        return root == null ? 0 : Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }
}

二叉树的最小深度

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/

问题叙述

给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明：叶子节点是指没有子节点的节点。

示例 1

输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示

树中节点数的范围在 [0, 10^5] 内
-1000 <= Node.val <= 1000

分析

题目中说 最小深度是从根节点到最近叶子节点的最短路径上的节点数量
而叶子节点是指没有子节点的节点
跟最大深度类似 每当遍历一层的时候 深度加一
所以我们一层一层遍历 找到一个叶子节点的时候 返回它的深度即可

Code

class Solution {
    public int minDepth(TreeNode root) {
        int depth = 0;
        if (root == null) return depth;
        LinkedList<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            depth++;
            for (int i = 0; i < size; i++) {
                TreeNode tmp = deque.pollFirst();
                if (tmp.left != null) deque.offer(tmp.left);
                if (tmp.right != null) deque.offer(tmp.right);
                if (tmp.left == null && tmp.right == null) return depth;
            }
        }
        return depth;
    }
}

在每个树行中找最大值

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/find-largest-value-in-each-tree-row/

问题叙述

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

示例1

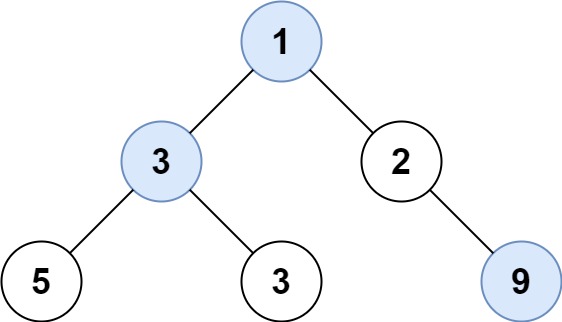
输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]

示例2

输入: root = [1,2,3]
输出: [1,3]

提示

二叉树的节点个数的范围是 [0,10^4]
-2^31 <= Node.val <= 2^31 - 1

分析

遍历每一层的时候 实时更新一下最大值即可

Code

class Solution {
    public List<Integer> largestValues(TreeNode root) {
        ArrayList<Integer> res = new ArrayList<>();
        if (root == null) return res;
        LinkedList<TreeNode> deque = new LinkedList<>();
        deque.add(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            int max = Integer.MIN_VALUE;
            for (int i = 0; i < size; i++) {
                TreeNode tmp = deque.poll();
                max = Math.max(max, tmp.val);
                if (tmp.left != null) deque.add(tmp.left);
                if (tmp.right != null) deque.add(tmp.right);
            }
            res.add(max);
        }
        return res;
    }
}

填充每个节点的下一个右侧节点指针

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node/

问题叙述

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。
初始状态下，所有 next 指针都被设置为 NULL。

示例 1

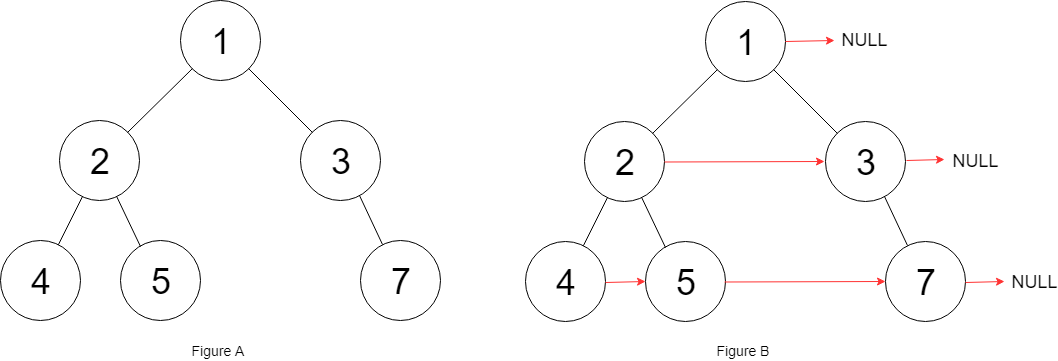
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，‘#’ 标志着每一层的结束。

示例 2

输入：root = []
输出：[]

提示

树中节点的数量在 [0, 2^12 - 1] 范围内
-1000 <= node.val <= 1000

进阶

你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

分析

每个元素出队的时候 让它的next指向队首元素即可 遍历到末尾元素时 让它指向null

Code

class Solution {
    public Node connect(Node root) {
        LinkedList<Node> deque = new LinkedList<>();
        if (root == null) return null;
        deque.offer(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            for (int i = 0; i < size; i++) {
                Node tmp = deque.pollFirst();
                if (i == size - 1) tmp.next = null;
                else tmp.next = deque.peek();
                if (tmp.left != null) deque.offer(tmp.left);
                if (tmp.right != null) deque.offer(tmp.right);

            }
        }
        return root;
    }
}

填充每个节点的下一个右侧节点指针II

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node-ii/

问题叙述

给定一个二叉树

struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

进阶

你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

示例

输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），‘#’ 表示每层的末尾。

提示

树中的节点数小于 6000
-100 <= node.val <= 100

分析

跟上题的代码一模一样

Code

class Solution {
    public Node connect(Node root) {
        LinkedList<Node> deque = new LinkedList<>();
        if (root == null) return null;
        deque.offer(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            for (int i = 0; i < size; i++) {
                Node tmp = deque.pollFirst();
                if (i == size - 1) tmp.next = null;
                else tmp.next = deque.peek();
                if (tmp.left != null) deque.offer(tmp.left);
                if (tmp.right != null) deque.offer(tmp.right);

            }
        }
        return root;
    }
}

完全二叉树的节点个数

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/count-complete-tree-nodes/

问题叙述

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。
完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1

输入：root = [1,2,3,4,5,6]
输出：6

示例 2

输入：root = []
输出：0

示例 3

输入：root = [1]
输出：1

提示

树中节点的数目范围是[0, 5 * 10^4]
0 <= Node.val <= 5 * 10^4
题目数据保证输入的树是 完全二叉树

进阶

遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗？

分析

Code

class Solution {
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        ArrayList<Integer> list = new ArrayList<>();
        LinkedList<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            for (int i = 0; i < size; i++) {
                TreeNode tmp = deque.pollFirst();
                list.add(tmp.val);
                if (tmp.left != null) deque.offer(tmp.left);
                if (tmp.right != null) deque.offer(tmp.right);
            }
        }
        return list.size();
    }
}

翻转二叉树

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/invert-binary-tree/

问题叙述

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1

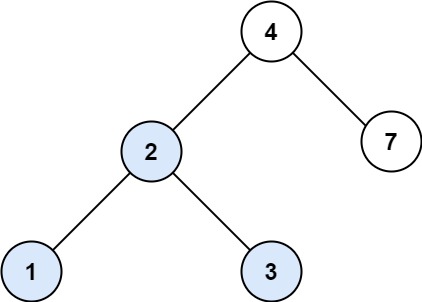
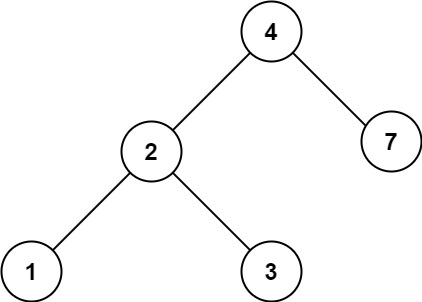
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2

输入：root = [2,1,3]
输出：[2,3,1]

示例 3

输入：root = []
输出：[]

提示

树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100

分析

层序遍历时 交换每个节点两个子节点即可

Code

class Solution {
    public TreeNode invertTree(TreeNode root) {
        LinkedList<TreeNode> deque = new LinkedList<>();
        if (root == null) return null;
        deque.offer(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            for (int i = 0; i < size; i++) {
                TreeNode tmp = deque.pollFirst();
                swapNode(tmp);
                if (tmp.left != null) deque.push(tmp.left);
                if (tmp.right != null) deque.push(tmp.right);
            }
        }
        return root;
    }

    void swapNode(TreeNode root) {
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
    }
}
//递归
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return null;
        TreeNode tmp;
        tmp = root.left;
        root.left = root.right;
        root.right = tmp;
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
}

对称二叉树

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/symmetric-tree/

问题叙述

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2

输入：root = [1,2,2,null,3,null,3]
输出：false

提示

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

分析

我们可以利用双端队列的特性 把他当成两个队列用
比较左右两边的节点是否对称 那我们把左边的节点从对头插入 右边的节点从队尾插入
节点入队的时候也要按对称的顺序

Code

//迭代
class Solution {
    public boolean isSymmetric(TreeNode root) {
        LinkedList<TreeNode> deque = new LinkedList<>();
        deque.offerFirst(root.left);
        deque.offerLast(root.right);
        while (!deque.isEmpty()) {
            TreeNode left = deque.pollFirst();
            TreeNode right = deque.pollLast();
            if (left == null && right == null) continue;
            if (left == null || right == null || left.val != right.val) return false;
            deque.offerFirst(left.left);
            deque.offerFirst(left.right);
            deque.offerLast(right.right);
            deque.offerLast(right.left);
        }
        return true;
    }
}
//递归
class Solution {
    public boolean isSymmetric(TreeNode root) {
        return CompareNode(root, root);
    }

    boolean CompareNode(TreeNode p, TreeNode q) {
        if (p == null && q == null) return true;
        if (p == null || q == null) return false;
        return p.val == q.val && CompareNode(p.left, q.right) && CompareNode(p.right, q.left);
    }
}

平衡二叉树

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/balanced-binary-tree/

问题叙述

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例1

输入：root = [3,9,20,null,null,15,7]
输出：true

示例2

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例3

输入：root = []
输出：true

提示

树中的节点数在范围 [0, 5000] 内
-10^4 <= Node.val <= 10^4

分析

对于当前遍历到的节点，先遍历它的左右子树是否平衡，再判断以当前节点为根节点的子树是否平衡，如果平衡，则返回它的高度，不平衡则返回-1(高度如果存在则必然大于等于0)，如果左子树或右子树有一个不平衡，或者左右子树高度差大于1，则整棵二叉树不平衡

Code

class Solution {
    public boolean isBalanced(TreeNode root) {
        return height(root) != -1;
    }

    int height(TreeNode root) {
        if (root == null) return 0;
        int left_Height = height(root.left);
        int right_Height = height(root.right);
        if (left_Height == -1 || right_Height == -1 || Math.abs(left_Height - right_Height) > 1) return -1;
        else return 1 + Math.max(left_Height, right_Height);
    }
}

二叉树的所有路径

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/binary-tree-paths/

问题叙述

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。

示例1

![])(https://assets.leetcode.com/uploads/2021/03/12/paths-tree.jpg)
输入：root = [1,2,3,null,5]
输出：[“1->2->5”,“1->3”]

示例2

输入：root = [1]
输出：[“1”]

提示

树中节点的数目在范围 [1, 100] 内
-100 <= Node.val <= 100

分析

DFS
在用深度优先搜索遍历二叉树时，我们只需要考虑当前节点和他的子节点

• 如果当前节点是叶子节点，那我们只需要在当前路径的末尾加上该节点，然后我们就得到了一条由根节点到叶子节点的路径，将路径加入到结果中即可
• 如果当前节点不是叶子节点，则在当前路径的末尾加上该节点，然后继续递归遍历该节点的子节点

Code

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> res = new ArrayList<>();
        Magic(root, "", res);
        return res;
    }

    void Magic(TreeNode root, String curPath, List<String> res) {
        if (root != null) {
            StringBuffer sb = new StringBuffer(curPath);
            sb.append(root.val);
            if (root.left == null && root.right == null)
                res.add(sb.toString());
            else {
                sb.append("->");
                Magic(root.left, sb.toString(), res);
                Magic(root.right, sb.toString(), res);
            }
        }
    }
}

左叶子之和

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/sum-of-left-leaves/

问题叙述

给定二叉树的根节点 root ，返回所有左叶子之和。

示例1

输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例2

输入: root = [1]
输出: 0

提示

节点数在 [1, 1000] 范围内
-1000 <= Node.val <= 1000

分析

判断每个节点的左节点是否为叶子节点，然后递归的求取左子树的左叶子之和，右子树的左叶子之和，相加便是整个树的左叶子之和

Code

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) return 0;
        int sum = 0;
        if (root.left != null && root.left.left == null && root.left.right == null)
            sum += root.left.val;
        return sum + sumOfLeftLeaves(root.left) + sumOfLeftLeaves(root.right);
    }
}

找树左下角的值

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/find-bottom-left-tree-value/

问题叙述

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。

示例1

输入: root = [2,1,3]
输出: 1

示例2

输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

提示

二叉树的节点个数的范围是 [1,10^4]
-2^31 <= Node.val <= 2^31 - 1

分析

层序遍历YYDS
我们需要找最底层最左边节点的值
那我们层序遍历时 从右往左遍历 遍历到的最后一个元素就是要找的节点

Code

class Solution {
    public int findBottomLeftValue(TreeNode root) {
        LinkedList<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        while (!deque.isEmpty()) {
            root = deque.poll();
            if (root.right != null) deque.offer(root.right);
            if (root.left != null) deque.offer(root.left);
        }
        return root.val;
    }
}

路径总和

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/path-sum/

问题叙述

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。
叶子节点 是指没有子节点的节点。

示例1

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例2

输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例3

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示

树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

分析

递归
如果当前节点是叶子节点，那我们可以直接判断val是否等于targetSum
如果当前节点不是叶子节点，那我们递归的判断他的子节点的val是否满足targetSum-val

Code

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root == null) return false;
        if (root.left == null && root.right == null) return targetSum == root.val;
        return hasPathSum(root.left, targetSum - root.val)
                || hasPathSum(root.right, targetSum - root.val);
    }
}

从中序和后序遍历构造二叉树

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/

问题叙述

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例2

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示

1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由 不同 的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历

分析

递归
终止条件是数组长度为0 也就是空节点
如果不为空 我们取后序遍历的最后一个节点作为根节点
我们按照这个根节点 可以把中序遍历数组分为左数组和右数组
同样 将后序遍历数组分为左数组和右数组
递归处理左区间和右区间
PS:题目中说 中序和后序遍历都是由不同的值构成 所以不用担心有重值的情况

Code

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        if (inorder.length == 0 || postorder.length == 0) return null;
        int n = postorder.length;
        TreeNode root = new TreeNode(postorder[n - 1]);
        for (int i = 0; i < n; i++) {
            if (inorder[i] == root.val) {
                root.left = buildTree(Arrays.copyOfRange(inorder, 0, i), Arrays.copyOfRange(postorder, 0, i));
                root.right = buildTree(Arrays.copyOfRange(inorder, i + 1, n), Arrays.copyOfRange(postorder, i, n - 1));
            }
        }
        return root;
    }
}

从前序和中序遍历序列构造二叉树

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/

问题叙述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列

分析

和上题没有本质上的区别

Code

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder.length == 0 || inorder.length == 0) return null;
        int n = preorder.length;
        TreeNode root = new TreeNode(preorder[0]);
        for (int i = 0; i < n; i++) {
            if (inorder[i] == root.val) {
                root.left = buildTree(Arrays.copyOfRange(preorder, 1, i + 1), Arrays.copyOfRange(inorder, 0, i));
                root.right = buildTree(Arrays.copyOfRange(preorder, i + 1, n), Arrays.copyOfRange(inorder, i + 1, n));
            }
        }
        return root;
    }
}

最大二叉树

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/maximum-binary-tree/

问题叙述

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
创建一个根节点，其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。

示例 1

输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：

• [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
  • [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
    • 空数组，无子节点。
    • [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
      • 空数组，无子节点。
      • 只有一个元素，所以子节点是一个值为 1 的节点。
  • [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
    • 只有一个元素，所以子节点是一个值为 0 的节点。
    • 空数组，无子节点。

示例 2

输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同

分析

题目中已经给了思路了 照做就行 跟上题类似

Code

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        if (nums.length == 0) return null;
        int maxIndex = findMaxIndex(nums);
        TreeNode root = new TreeNode(nums[maxIndex]);
        root.left = constructMaximumBinaryTree(Arrays.copyOfRange(nums, 0, maxIndex));
        root.right = constructMaximumBinaryTree(Arrays.copyOfRange(nums, maxIndex + 1, nums.length));
        return root;
    }

    int findMaxIndex(int[] nums) {
        int index = -1;
        int max = -1;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] > max) {
                max = nums[i];
                index = i;
            }
        }
        return index;
    }
}

合并二叉树

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/merge-two-binary-trees/

问题叙述

给你两棵二叉树： root1 和 root2 。
想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。

示例 1

输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

提示

两棵树中的节点数目在范围 [0, 2000] 内
-10^4 <= Node.val <= 10^4

分析

合并两棵树
如果root1是null 那就返回root2即可(root2是null也无所谓 反正也是返回null)
如果root2是null 那就返回root1
剩下的情况就是 root1和root2都不是null
那就把他们的值相加 合并成新节点
然后再用前序遍历递归处理即可(中序后序也可以)

Code

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null && root2 == null) return null;
        TreeNode root = null;
        if (root1 != null && root2 != null)
            root = new TreeNode(root1.val + root2.val);
        if (root1 == null) return root2;
        if (root2 == null) return root1;
        root.left = mergeTrees(root1.left, root2.left);
        root.right = mergeTrees(root1.right, root2.right);
        return root;
    }
}
//简化版 直接在root1或root2上修改也行
class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null) return root2;
        if (root2 == null) return root1;
        root1.val += root2.val;
        root1.left = mergeTrees(root1.left, root2.left);
        root1.right = mergeTrees(root1.right, root2.right);
        return root1;
    }
}

二叉搜索树中的搜索

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/search-in-a-binary-search-tree/

问题叙述

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

示例 1

输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2

输入：root = [4,2,7,1,3], val = 5
输出：[]

提示

数中节点数在 [1, 5000] 范围内
1 <= Node.val <= 10^7
root 是二叉搜索树
1 <= val <= 10^7

分析

先来说一下什么叫二叉搜索树
在二叉搜索树中：

1. 若任意结点的左子树不空，则左子树上所有结点的值均不大于它的根结点的值。
2. 若任意结点的右子树不空，则右子树上所有结点的值均不小于它的根结点的值。
3. 任意结点的左、右子树也分别为二叉搜索树。
4. 二叉搜索树的中序遍历是升序
   根据二叉搜索树的性质 如果要找的val值大于根节点的值 那val只可能在该根节点的右子树上找到
   同理 如果要找的val值小于根节点的值 那val只可能在该根节点的左子树上找到

Code

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null) return null;
        if (root.val == val) return root;
        if (root.val > val) return searchBST(root.left, val);
        if (root.val < val) return searchBST(root.right, val);
        return null;
    }
}
//简化版 前两条if语句可以合并
class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null || root.val == val) return root;
        if (root.val > val) return searchBST(root.left, val);
        if (root.val < val) return searchBST(root.right, val);
        return null;
    }
}

验证二叉搜索树

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/validate-binary-search-tree/

问题叙述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下：
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1

输入：root = [2,1,3]
输出：true

示例2

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示

树中节点数目范围在[1, 10^4] 内
-2^31 <= Node.val <= 2^31 - 1

分析

二叉搜索树的中序遍历是升序的
所以我们用中序遍历二叉搜索树
如果当且节点值小于等于上一节点值 则满足条件
否则则不是二叉搜索树

Code

class Solution {
    long pre = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        if (!isValidBST(root.left)) return true;
        if (root.val <= pre)
            return false;
        pre = root.val;
        return isValidBST(root.right);
    }
}

二叉搜索树的最小绝对值差

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/minimum-absolute-difference-in-bst/

问题叙述

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数，其数值等于两值之差的绝对值。

示例 1

输入：root = [4,2,6,1,3]
输出：1

示例2

输入：root = [1,0,48,null,null,12,49]
输出：1

提示

树中节点的数目范围是 [2, 104]
0 <= Node.val <= 105

分析

题目要求找任意两节点之差绝对值的最小值
由于中序遍历的顺序是升序的 所以最小绝对值差 只可能是中序遍历序列中两个相邻元素之差

Code

class Solution {
    public int getMinimumDifference(TreeNode root) {
        ArrayList<Integer> list = new ArrayList<>();
        inorder(root, list);
        int min = Integer.MAX_VALUE;
        for (int i = 0; i < list.size() - 1; i++) {
            min = Math.min(list.get(i + 1) - list.get(i), min);
        }
        return min;
    }

    void inorder(TreeNode root, ArrayList<Integer> list) {
        if (root == null) return;
        inorder(root.left, list);
        list.add(root.val);
        inorder(root.right, list);
    }
}

二叉搜索树中的众数

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/find-mode-in-binary-search-tree/

问题叙述

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。
如果树中有不止一个众数，可以按 任意顺序 返回。
假定 BST 满足如下定义：

1. 结点左子树中所含节点的值 小于等于 当前节点的值
2. 结点右子树中所含节点的值 大于等于 当前节点的值
3. 左子树和右子树都是二叉搜索树

示例 1

输入：root = [1,null,2,2]
输出：[2]

示例 2

输入：root = [0]
输出：[0]

提示

树中节点的数目在范围 [1, 10^4] 内
-10^5 <= Node.val <= 10^5
进阶：你可以不使用额外的空间吗？（假设由递归产生的隐式调用栈的开销不被计算在内）

分析

中序遍历是有序序列
所以这道题就简化为从有序序列中寻找众数
用pre记录当前节点的上一个节点 初始化为null
count记录当前数字重复次数
maxCount表示已经扫描过的数字中出现的最大次数
如果pre和root的值相同，也就是当前节点与上一个节点的值相等 则count++
pre为null时 是判断第一个节点 此时执行count++也没问题
否则 则将count初始化为1
然后将root赋给pre
接着比较当前的count和maxCount
如果二者相等 则有多个众数 将当前节点的val加入到结果中
如果当前的count大于maxCount 则说明出现了新的众数 将原有结果清空 同时将maxCount更新为当前count 将该节点的val加入到结果中

Code

class Solution {
    int count = 0;
    int maxCount = 0;
    TreeNode pre = null;

    public int[] findMode(TreeNode root) {
        ArrayList<Integer> list = new ArrayList<>();
        inorder(root, list);
        int[] res = new int[list.size()];
        for (int i = 0; i < list.size(); i++) {
            res[i] = list.get(i);
        }
        return res;
    }

    void inorder(TreeNode root, ArrayList<Integer> list) {
        if (root == null) return;
        inorder(root.left, list);
        if (pre == null || pre.val == root.val) {
            count++;
        } else {
            count = 1;
        }
        pre = root;
        if (count == maxCount) {
            list.add(root.val);
        } else if (count > maxCount) {
            list.clear();
            maxCount = count;
            list.add(root.val);
        }
        inorder(root.right, list);
    }
}

二叉树的最近公共祖先

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/

问题叙述

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3

输入：root = [1,2], p = 1, q = 2
输出：1

提示

树中节点数目在范围 [2, 10^5] 内。
-10^9 <= Node.val <= 10^9
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。

分析

递归
若 root 是 p, q 的 最近公共祖先 ，则只可能为以下情况之一：

1. p 和 q 在 root 的子树中，且分列 root 的 异侧（即分别在左、右子树中）；
2. p = root，且 q 在 root 的左或右子树中；
3. q = root，且 p 在 root 的左或右子树中；

后序遍历整棵二叉树
用 left 和 right 分别表示 当前节点的左子树或右子树是否包含节点p或 q ，如果包含为true 否则为false
那么符合条件的最近公共祖先则满足以下条件:
(left && right) || ((root == p || root == q) && (left || right))
(left && right)对应情况1 p和q分裂当前root节点的异侧
(root == p || root == q) && (left || right) 对应条件2和3
由于我们是自底向顶遍历的 所以我们找到满足root == p || root == q的节点时 要判断它的左子树或右子树是否包含另一个节点
由于我们是自底向顶遍历的 所以满足条件的root必然是深度最大的 也就是最近的公共祖先

Code

class Solution {
    TreeNode res = null;

    boolean hasPorQ(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) return false;
        boolean left = hasPorQ(root.left, p, q);
        boolean right = hasPorQ(root.right, p, q);
        if ((left && right) || ((root == p || root == q) && (left || right)))
            res = root;
        return left || right || root.val == p.val || root.val == q.val;
    }

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        hasPorQ(root, p, q);
        return res;
    }
}

二叉搜索树的最近公共祖先

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-search-tree/

问题叙述

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”
例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

分析

利用二叉搜索树的性质
左子树中所含节点的值 小于等于 当前节点的值
右子树中所含节点的值 大于等于 当前节点的值
从根节点开始遍历
如果当前节点的值大于p和q的值 那么p和q则应该在当前节点的左子树上 所以我们把当前节点移到它的左子节点上
如果当前节点的值小于p和q的值 那么p和q则应该在当前节点的右子树上 所以我们把当前节点移到它的右子节点上
如果不满足上述两条要求 则说明p和q分布在当前节点两侧 或者当前节点是p或q 满足要求 返回当前节点即可

直接用上题的代码也可以

Code

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        while (true) {
            if (root.val > p.val && root.val > q.val)
                root = root.left;
            else if (root.val < p.val && root.val < q.val)
                root = root.right;
            else break;
        }
        return root;
    }
}

二叉搜索树中的插入操作

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/insert-into-a-binary-search-tree/

问题叙述

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。
注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1

输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

示例 2

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]

示例 3

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

提示

树中的节点数将在 [0, 10^4]的范围内。
-10^8 <= Node.val <= 10^8
所有值 Node.val 是 独一无二 的。
-10^8 <= val <= 10^8
保证 val 在原始BST中不存在。

分析

递归
比较root.val和目标val的大小关系
如果root.val大于目标val 则说明需要插入到左子树中
如果root.val小于目标val 则说明需要插入到右子树中
如果此时的左/右子树为null 则表明可以直接插入 返回新建一个目标val的节点即可
否则的话 继续执行上述两步 直至找到一个合适的位置可供插入

Code

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) return new TreeNode(val);
        if (val < root.val) root.left = insertIntoBST(root.left, val);
        if (val > root.val) root.right = insertIntoBST(root.right, val);
        return root;
    }
}

删除二叉搜索树中的节点

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/delete-node-in-a-bst/

问题叙述

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。
一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

示例 1

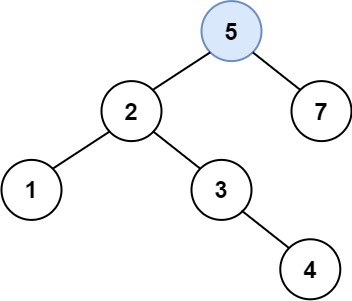
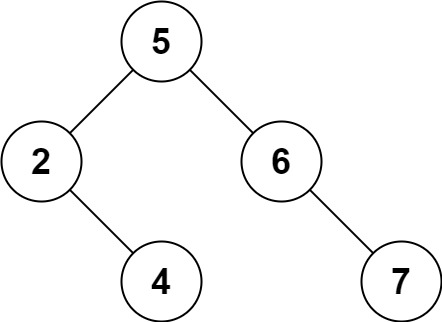
输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3

输入: root = [], key = 0
输出: []

提示

节点数的范围 [0, 10^4].
-10^5 <= Node.val <= 10^5
节点值唯一
root 是合法的二叉搜索树
-10^5 <= key <= 10^5

分析

递归

1. 没找到删除节点 返回原来的根节点即可
2. 找到了目标节点 目标节点的两个孩子都不存在 那我们执行root=null:
3. 找到了目标节点 目标节点的左孩子是null 那就直接把目标节点的right 替换到当前节点 root=root.right:
4. 找到了目标节点 目标节点的右孩子是null 那就直接把目标节点的left 替换到当前节点 root=root.left:
5. 找到了目标节点 目标节点的左右孩子均存在 由于二叉搜索树的中序遍历是递增的 那目标节点的左孩子树的所有值均小于右孩子树的最小值 所以我们找到右孩子树上的最左节点 也就是右孩子树上最小的节点 我们将目标节点的左孩子放在右孩子树上最小节点的左孩子的位置 就能满足题目要求

Code

class Solution {

    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) return null;
        if (root.val > key) root.left = deleteNode(root.left, key);
        if (root.val < key) root.right = deleteNode(root.right, key);
        if (root.val == key) {
            if (root.left == null && root.right == null) root = null;
            else if (root.left == null) root = root.right;
            else if (root.right == null) root = root.left;
            else {
                TreeNode node = root.right;
                while (node.left != null) node = node.left;
                node.left = root.left;
                root = root.right;
            }
        }
        return root;
    }
}

修剪二叉搜索树

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/trim-a-binary-search-tree/

问题叙述

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1

输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例 2

输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

提示

树中节点数在范围 [1, 10^4] 内
0 <= Node.val <= 10^4
树中每个节点的值都是 唯一 的
题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 10^4

分析

Code

//
class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null) return null;
        //如果当前节点的值 比左区间端点还小 那就尝试一下当前节点的右节点
        if (root.val < low) {
            root = root.right;
            root = trimBST(root, low, high);
        //如果当前节点的值 比右区间断电还大 那就尝试一下当前节点的左节点
        } else if (root.val > high) {
            root = root.left;
            root = trimBST(root, low, high);
        }
        //当前节点满足在区间内 那就先序遍历递归处理所有节点
        else {
            root.left = trimBST(root.left, low, high);
            root.right = trimBST(root.right, low, high);
        }
        return root;
    }
}
//简洁版本
class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null) return null;
        if (root.val < low) return trimBST(root.right, low, high);
        if (root.val > high) return trimBST(root.left, low, high);
        root.left = trimBST(root.left, low, high);
        root.right = trimBST(root.right, low, high);
        return root;
    }
}

将有序数组转化为二叉搜索树

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree/

问题叙述

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2

输入：nums = [1,3]
输出：[3,1]
解释：[1,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示

1 <= nums.length <= 10^4
-10^4 <= nums[i] <= 10^4
nums 按 严格递增 顺序排列

分析

二分 每次找出数组最中间的值 令它作为根节点

Code

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return nums.length == 0 ? null : Magic(nums, 0, nums.length - 1);
    }

    TreeNode Magic(int[] nums, int left, int right) {
        if (left > right) return null;
        int mid = ((right + left) >> 1);
        TreeNode root = new TreeNode(nums[mid]);
        root.left = Magic(nums, left, mid - 1);
        root.left = Magic(nums, mid + 1, right);
        return root;
    }
}

把二叉搜索树转化为累加树

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/convert-bst-to-greater-tree/

问题叙述

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下，二叉搜索树满足下列约束条件：
节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。
注意：本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

示例 1

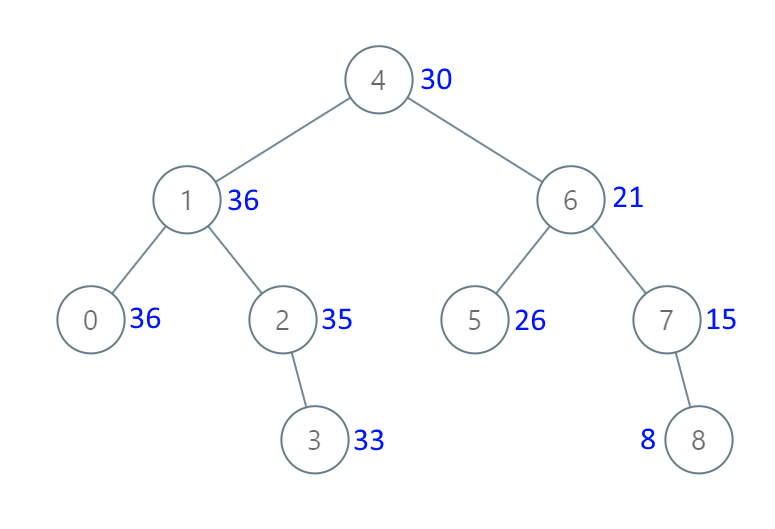
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2

输入：root = [0,null,1]
输出：[1,null,1]

示例 3

输入：root = [1,0,2]
输出：[3,3,2]

示例 4

输入：root = [3,2,4,1]
输出：[7,9,4,10]

提示

树中的节点数介于 0 和 10^4 之间。
每个节点的值介于 -10^4 和 10^4 之间。
树中的所有值 互不相同 。
给定的树为二叉搜索树。

分析

读不懂题 然后我去看了1038题 总算读懂了
给定一个二叉搜索树 root (BST)，请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。
由于中序遍历是递增的 左边到右边依次增大
所以每个节点的值是 本身+右边所有节点
所以我们从右往左进行中序遍历即可 每个节点的值 都等于 自身+上一个节点

Code

class Solution {
    int num = 0;

    public TreeNode convertBST(TreeNode root) {
        if (root == null) return null;
        convertBST(root.right);
        num += root.val;
        root.val = num;
        convertBST(root.left);
        return root;
    }
}