印章

资源限制

时间限制：1.0s 内存限制：256.0MB

问题叙述

共有n种图案的印章，每种图案的出现概率相同。小A买了m张印章，求小A集齐n种印章的概率。

输入格式

一行两个正整数n和m

输出格式

一个实数P表示答案，保留4位小数。

样例输入

2 3

样例输出

0.7500

数据规模和约定

1≤n，m≤20

思路分析

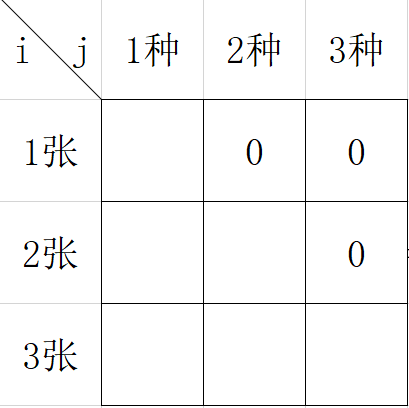
首先建立一个二维数组 dp[m][n]
数组中的每个元素dp[i][j]表示买i张集齐j种的概率(假设数组下标从1开始，方便理解)
假设有3种图案，买了3张。
我们先来看一般情况：

分析：n种图案，买m张，买到每种图案的概率p=1/n。当买的张数比图案总数小的时候，那必然不能集齐。也就是当i<j时，dp[i][j]=0。
i<j
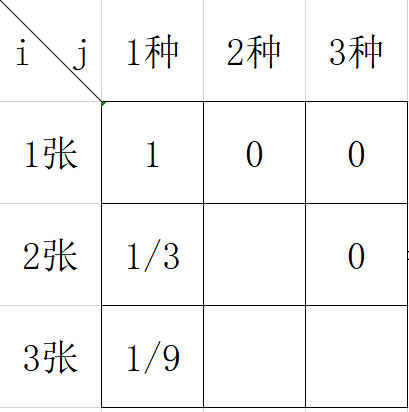
分析：当j=1时，也就是凑齐一种即可，买一张凑齐一种的概率是1，买两张凑齐一种(这一种是任意一种，所以概率要乘以n)的概率是p^2*n，买i张凑齐一种的概率是p^i*n，又p=1/n，故买i张凑齐1中的概率是p^(i-1)。
j=1
然后再看看其他情况：
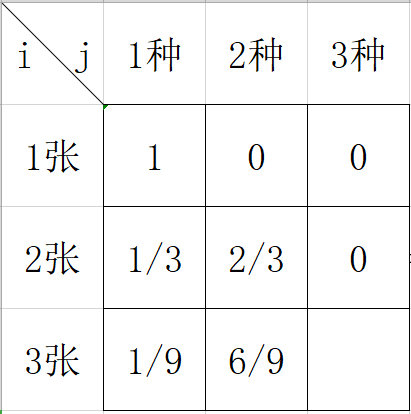
分析；当我们想计算2张2种的情况时，可以由1张1种的基础上，再买到不同于这1张的其余两张，也就是dp[2][2]=dp[1][1]*p*2=2/3。
当我们想计算3张2种的情况是，可以由2张2种的基础上，再买到1种已拥有的，或者由2张1种的情况下，买到1种未拥有的，也就是dp[3][2]=dp[2][2]*p*2+dp[2][1]*p*2=6/9。综上所述，dp[i][j]=dp[i-1][j]*(j*p)+dp[i-1][j-1]*(n-j+1)*p;(注：此解的数组下标从1开始，下文的Java代码数组下标从0开始)
其余情况
依次类推就能计算出3张3种的结果了。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import java.text.DecimalFormat;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        int m = scan.nextInt();
        double p = 1.0 / n;
        double[][] dp = new double[m][n];
        DecimalFormat df = new DecimalFormat("0.0000");
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (i < j) {
                    dp[i][j] = 0;
                } else if (j == 0) {
                    dp[i][j] = Math.pow(p, i);
                } else if (i > 0)
                    dp[i][j] = dp[i - 1][j] * p * (j + 1) + dp[i - 1][j - 1] * (n - j) * p;

            }
        }
        System.out.println(df.format(dp[m - 1][n - 1]));
    }
}

拿金币

资源限制

时间限制：1.0s 内存限制：256.0MB

问题叙述

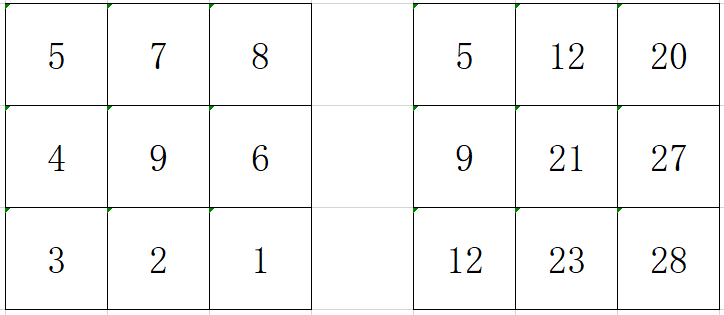
有一个N x N的方格,每一个格子都有一些金币,只要站在格子里就能拿到里面的金币。你站在最左上角的格子里,每次可以从一个格子走到它右边或下边的格子里。请问如何走才能拿到最多的金币。

输入格式

第一行输入一个正整数n。
以下n行描述该方格。金币数保证是不超过1000的正整数。

输出格式

最多能拿金币数量。

样例输入

3
1 3 3
2 2 2
3 1 2

样例输出

11

数据规模和约定

n<=1000

思路分析

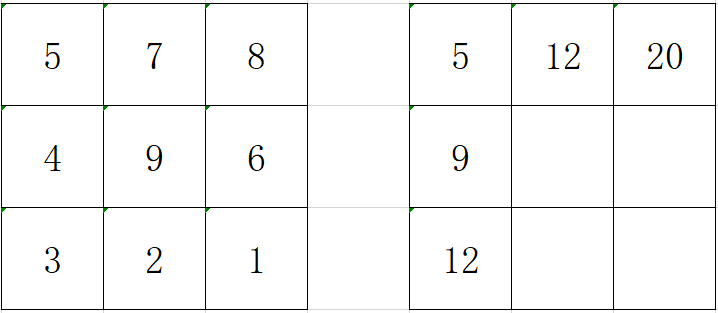
跟上题一样，先建立一个二维数组dp[n][n]
数组中的每个元素dp[i][j]表示到达该位置时，所获得的最大金币数。

分析：一层一层遍历就好了，当j==0时，也就是在第一行，每个格子所获得的的最大金币数即为：本格子的金币数，加上左边格子所获得的的最大金币数，arr[i][j] += arr[i][j - 1];
当i==0时，也就是在第一列，第一列的每个格子能获取到的最大金币数为：本格子的金币数，加上上方格子的获取到的最大金币数，arr[i][j] += arr[i - 1][j];。（图示仅限于方便理解，实际上是一层一层出结果的，不是图中先把第一行第一列的结果算完。）
一条道走到黑
当我们算到中间格子时，就出现了选择，要想获取最大金币数，那就应该用本格的金币数，加上MAX（上边格子，左边格子），很显然选择上边格子能获取到最大金币数。也就是
arr[i][j] += Math.max(arr[i - 1][j], arr[i][j - 1]);
最优吃金币

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        int[][] dp = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                dp[i][j] = scan.nextInt();
            }
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (i == 0 && j > 0) {
                    dp[i][j] += dp[i][j - 1];
                } else if (j == 0 && i > 0) {
                    dp[i][j] += dp[i - 1][j];
                } else if(i>0)
                    dp[i][j] += Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
        System.out.println(dp[n-1][n-1]);
    }
}

摆动序列

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/wiggle-subsequence

问题叙述

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 摆动序列 。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。
给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

示例 1

输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

示例 2

输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7

解释：这个序列包含几个长度为 7 摆动序列。

其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。

示例 3

输入：nums = [1,2,3,4,5,6,7,8,9]
输出：2

提示

1 <= nums.length <= 1000
0 <= nums[i] <= 1000

思路分析

up[i]表示 从0~i中 最后两个数字是递增的最长摆动序列
down[i]表示 从0~i中 最后两个数字是递减的最长摆动序列
下面进行分类讨论
nums[i+1]>nums[i] 最后两个数字是递增的 nums[i-1]和nums[i]

拿示例2举例

17>1 up = down+1 = 2
5<17 down = up+1 = 3
10>5 up = down+1 = 4
13>10 up = down+1 = 4
15>13 up = down+1 = 4
10<15 down = up+1 = 5
5<10 down = up+1 = 5
16>5 up = down+1 = 6
8<16 down = up+1 = 7
连续的up操作或者down操作是无效的 数据不会更新
只有up和down交替操作 数据才会更新 从而达到摆动序列的效果

Code

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int wiggleMaxLength(int[] nums) {
        int up = 1, down = 1;
        for (int i = 0; i < nums.length - 1; i++) {
            if (nums[i] > nums[i + 1])
                up = down + 1;
            if (nums[i] < nums[i + 1])
                down = up + 1;
        }
        return nums.length == 0 ? 0 : Math.max(up, down);
    }
}

最大子序列和

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-subarray

问题叙述

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
子数组 是数组中的一个连续部分。

示例 1

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2

输入：nums = [1]
输出：1

示例 3

输入：nums = [5,4,-1,7,8]
输出：23

提示

1 <= nums.length <= 105
-104 <= nums[i] <= 104

思路分析

创建一个等长的一维数组dp[nums.length]
数组中的每一个元素dp[i]是以nums[i]结尾的最大子序列和
初始化dp[0]=nums[0]
则状态转移方程为dp[i]=Math.max(dp[i-1]+nums[i],nums[i])
每次遍历完一个元素之后 实时保存一下最大值 最后作为结果返回即可

Code

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int maxSubArray(int[] nums) {
        int[] dp = new int[nums.length];
        int max = nums[0];
        dp[0] = nums[0];
        for (int i = 1; i < nums.length; i++) {
            dp[i]=Math.max(nums[i], dp[i - 1]+nums[i]);
            max = Math.max(max, dp[i]);
        }
        return max;
    }
}

斐波那契数

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/fibonacci-number/

问题叙述

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：
F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给定 n ，请计算 F(n) 。

示例 1

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3

输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

提示

0 <= n <= 30

思路分析

状态转移方程题目中已经给出
F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

Code

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int fib(int n) {
        int[] dp = new int[n + 1];
        if (n < 2) return n;
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

爬楼梯

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/climbing-stairs/

问题叙述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。

  • 1 阶 + 1 阶
  • 2 阶

示例 2

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。

  • 1 阶 + 1 阶 + 1 阶
  • 1 阶 + 2 阶
  • 2 阶 + 1 阶

提示

1 <= n <= 45

思路分析

dp[i]表示到达第i阶台阶的种数
到达第i阶台阶 只能由第i-1阶走一步 或者i-2阶走两步
所以到第i阶的种数 就是第i-1阶和第i-2阶的种数之和
状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];
初始化 dp[1] = 1; dp[2] = 2;

Code

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int climbStairs(int n) {
        int[] dp = new int[n + 1];
        if (n <= 2) return n;
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

使用最小花费爬楼梯

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/min-cost-climbing-stairs/

问题叙述

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。

示例 1

输入：cost = [10,15,20]
输出：15
解释：你将从下标为 1 的台阶开始。
支付 15 ，向上爬两个台阶，到达楼梯顶部。
总花费为 15 。

示例 2

输入：cost = [1,100,1,1,1,100,1,1,100,1]
输出：6
解释：你将从下标为 0 的台阶开始。

  • 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
  • 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
  • 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
  • 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
  • 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
  • 支付 1 ，向上爬一个台阶，到达楼梯顶部。
    总花费为 6 。

提示

2 <= cost.length <= 1000
0 <= cost[i] <= 999

思路分析

dp[i]表示到达第i阶台阶的最小花费
由于可以从下标0或下标1起步
那么就可以初始化dp[0] = 0; dp[1] = 0;
状态转移方程 dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
到达第i阶台阶
可以由第i-1阶台阶 花费cost[i-1]到达
也可由第i-2阶台阶 花费cost[i-2]到达
从二者中取最小值

Code

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int[] dp = new int[cost.length + 1];
        dp[0] = 0;
        dp[1] = 0;
        for (int i = 2; i <= cost.length; i++) {
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[cost.length];
    }
}

不同路径

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/unique-paths/

问题叙述

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。
问总共有多少条不同的路径？

示例 1


输入：m = 3, n = 7
输出：28

示例 2

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。

  1. 向右 -> 向下 -> 向下
  2. 向下 -> 向下 -> 向右
  3. 向下 -> 向右 -> 向下

示例 3

输入：m = 7, n = 3
输出：28

示例 4

输入：m = 3, n = 3
输出：6

提示

1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9

思路分析

dp[i][j]表示 走到第i行第j列 的路径条数
第一行和第一列只有一种走法 所以初始化为1即可
由于只能往右走和往下走
所以每个位置 只能由其上方或者左方走来
所以状态转移方程为 dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

Code

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for (int i = 0; i < m; i++) dp[i][0] = 1;
        for (int j = 0; j < n; j++) dp[0][j] = 1;
        for (int i = 1; i < m; i++)
            for (int j = 1; j < n; j++)
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        return dp[m - 1][n - 1];
    }
}

不同路径II

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/unique-paths-ii/

问题叙述

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？
网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1


输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：

  1. 向右 -> 向右 -> 向下 -> 向下
  2. 向下 -> 向下 -> 向右 -> 向右

示例 2


输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示

m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1

思路分析

跟上题一样 不过在初始化时 需要判断当前位置不是障碍物

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];
        for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
        for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
        for (int i = 1; i < m; i++)
            for (int j = 1; j < n; j++)
                if (obstacleGrid[i][j] == 0)
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        return dp[m - 1][n - 1];
    }
}

整数拆分

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/integer-break/

问题叙述

给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。

示例 1

输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 1

输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

提示

2 <= n <= 58

思路分析

dp[i] 表示将i拆解为若干个整数 获得的最大乘积值
由于题目中的范围是[2,58]
所以我们先初始化 dp[2] = 1;
如何得到dp[i]
j从1到i-1遍历
dp[i] = i * (i - j) 或者 dp[i] = j * dp[i - j]
每次遍历从中取最大值
所以状态转移方程为 dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));

Code

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int integerBreak(int n) {
        int[] dp = new int[n + 1];
        dp[2] = 1;
        for (int i = 3; i < n + 1; i++) {
            for (int j = 1; j < i; j++) {
                dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
            }
        }
        return dp[n];
    }
}

分割等和子集

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/partition-equal-subset-sum/

问题叙述

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1

输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2

输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

提示

1 <= nums.length <= 200
1 <= nums[i] <= 100

思路分析

转化为01背包问题
dp[j]表示容量为j的背包 从前i个元素中任取 能装下的最大物品之和
如果数组之和为奇数 则不可能分为两个和相等的子集 直接return false;
最终我们判断容量为sum/2的背包 最多能装下多少物品
也就是 return dp[sum/2] == sum/2;

状态转移方程分析
每种数字只有取与不取两种状态
如果不取的话 那么dp[j]保持上一步的状态即可
如果取的话 需要腾出对应的空间 也就是在dp[j-nums[i]]的基础上 数字所占空间nums[i]
所以状态转移方程为
一维：dp[j] = Math.max(dp[j], dp[j - num] + num);
二维：dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i]);

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
//一维DP
class Solution {
    public boolean canPartition(int[] nums) {
        int sum = 0;
        for (int num : nums) sum += num;
        if (sum % 2 == 1) return false;
        int target = sum >> 1;
        int[] dp = new int[target + 1];
        for (int num : nums) {
            for (int j = target; j >= num; j--) {
                dp[j] = Math.max(dp[j], dp[j - num] + num);
            }
        }
        return dp[target] == target;
    }
}
//二维DP
class Solution {
    public boolean canPartition(int[] nums) {
        int sum = 0;
        for (int num : nums) sum += num;
        if (sum % 2 == 1) return false;
        int target = sum / 2;
        int[][] dp = new int[nums.length][target + 1];

        for (int j = nums[0]; j <= target; j++) {
            dp[0][j] = nums[0];
        }

        for (int i = 1; i < nums.length; i++) {
            for (int j = 0; j < target + 1; j++) {
                if (j >= nums[i])
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i]);
                else dp[i][j] = dp[i - 1][j];
            }
        }

        return dp[nums.length - 1][target] == target;
    }
}

最后一块石头的重量II

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/last-stone-weight-ii/

问题叙述

有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：
如果 x == y，那么两块石头都会被完全粉碎；
如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。
最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

示例 1

输入：stones = [2,7,4,1,8,1]
输出：1
解释：
组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

示例 2

输入：stones = [31,26,33,21,40]
输出：5

示例 3

输入：stones = [1,2]
输出：1

提示

1 <= stones.length <= 30
1 <= stones[i] <= 100

思路分析

转化为01背包问题
题目想要最后一块石头的重量最小
那我们就把石头分成两堆 使两堆石头的质量差值最小即可
那我们就可以把问题转化为 容量为sum/2的背包 最多能装下多重的石头
设这背包的最大重量为A
那另一堆的重量为sum-A
题目所求则是 sum-A-A=sum-2A
将sum-2A作为最终结果返回即可

状态转移方程分析
每种物品只有取与不取两种状态
如果不取的话 那么dp[j]保持上一步的状态即可
如果取的话 需要腾出对应的空间 也就是在dp[j-stones[i]]的基础上 加上石头的质量stones[i]
所以状态转移方程为
一维：dp[j] = Math.max(dp[j], dp[j - num] + num);
二维：dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i]);

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
//一维DP
class Solution {
    public int lastStoneWeightII(int[] stones) {
        int sum = 0;
        for (int stone : stones) {
            sum += stone;
        }
        int target = sum / 2;
        int[] dp = new int[target + 1];
        for (int i = 0; i < stones.length; i++) {
            for (int j = target; j >= stones[i]; j--) {
                dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
            }
        }
        return sum - 2 * dp[target];
    }
}
//二维DP
class Solution {
    public int lastStoneWeightII(int[] stones) {
        int sum = 0;
        for (int stone : stones) {
            sum += stone;
        }
        int target = sum / 2;
        int[][] dp = new int[stones.length][target + 1];
        for (int j = stones[0]; j <= target; j++) {
            dp[0][j] = stones[0];
        }
        for (int i = 1; i < stones.length; i++) {
            for (int j = 0; j < target + 1; j++) {
                if (j >= stones[i])
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - stones[i]] + stones[i]);
                else dp[i][j] = dp[i - 1][j];
            }
        }

        return sum - 2 * dp[stones.length - 1][target];
    }
}

目标和

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/target-sum/

问题叙述

给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ，然后串联起所有整数，可以构造一个 表达式 ：
例如，nums = [2, 1] ，可以在 2 之前添加 ‘+’ ，在 1 之前添加 ‘-’ ，然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

示例 1

输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

示例 2

输入：nums = [1], target = 1
输出：1

提示

1 <= nums.length <= 20
0 <= nums[i] <= 1000
0 <= sum(nums[i]) <= 1000
-1000 <= target <= 1000

思路分析

转化为01背包问题
题目意思是 随便加 加减符号 求凑出某个数的方法数
那我们就可以把这堆数 分为两个子集 然后做差 使差值为target
两个子集A和B
A + B = sum
A - B = target
2 * A = sum + target
A = (sum + target) / 2
每个A都对应着唯一的B和target 所以我们求出能凑出A的所有子集种类即可
dp[j] 表示填满容量为j的背包 有多少种方法
填满容量为j - nums[i]的背包，有dp[j - nums[i]]种方法。
所以状态转移方程为 dp[j] += dp[j - nums[i]]

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sum = 0;
        for (int i = 0; i < nums.length; i++) sum += nums[i];
        if ((target + sum) % 2 != 0) return 0;
        int size = (target + sum) / 2;
        if(size < 0) size = -size;
        int[] dp = new int[size + 1];
        dp[0] = 1;
        for (int i = 0; i < nums.length; i++) {
            for (int j = size; j >= nums[i]; j--) {
                dp[j] += dp[j - nums[i]];
            }
        }
        return dp[size];
    }
}

一和零

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/ones-and-zeroes/

问题叙述

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

示例 1

输入：strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,“0001”,“1”,“0”} ，因此答案是 4 。
其他满足题意但较小的子集包括 {“0001”,“1”} 和 {“10”,“1”,“0”} 。{“111001”} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

示例 2

输入：strs = [“10”, “0”, “1”], m = 1, n = 1
输出：2
解释：最大的子集是 {“0”, “1”} ，所以答案是 2 。

提示

1 <= strs.length <= 600
1 <= strs[i].length <= 100
strs[i] 仅由 ‘0’ 和 ‘1’ 组成
1 <= m, n <= 100

思路分析

转化为01背包问题 只不过有两个背包容量
dp[i][j]表示 使用i个0 j个1的情况下，可以得到的最大字符串数量
如果i < 当前字符串的ZeroCount 或者 j < 当前字符串的OneCount 则不能选取当前字符串 dp[i][j]保持不变
如果i >= 当前字符串的ZeroCount 且 j >= 当前字符串的OneCount 则可以选取当前字符串 也就是dp[i - ZeroCount][j - OneCount]+1
从这两种情况中 取最大字符串数量
所以状态转移方程为 dp[i][j] = Math.max(dp[i - OneCount][j - ZeroCount]+1, dp[i][j]);

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int[][] dp = new int[m + 1][n + 1];
        for (String str : strs) {
            int ZeroCount = 0, OneCount = 0;
            for (char c : str.toCharArray()) {
                if (c == '0') ZeroCount++;
                else OneCount++;
            }
            for (int i = m; i >= ZeroCount; i--) {
                for (int j = n; j >= OneCount; j--) {
                    dp[i][j] = Math.max(dp[i][j], dp[i - ZeroCount][j - OneCount] + 1);
                }
            }
        }
        return dp[m][n];
    }
}

零钱兑换II

来源：力扣（Leetcode）
链接：https://leetcode-cn.com/problems/coin-change-2/

问题叙述

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。

示例 1

输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

示例 2

输入：amount = 3, coins = [2]
输出：0
解释：只用面额 2 的硬币不能凑成总金额 3 。

示例 3

输入：amount = 10, coins = [10]
输出：1

提示

1 <= coins.length <= 300
1 <= coins[i] <= 5000
coins 中的所有值 互不相同
0 <= amount <= 5000

思路分析

完全背包问题 每个元素可以无限取 正序遍历
dp[j] 表示凑成总金额j的货币组合数为 dp[j]
dp[j] 就是所有的dp[j - coins[i]]相加
所以状态转移方程为：dp[j] += dp[j - coins[i]];

Code

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int change(int amount, int[] coins) {
        int[] dp = new int[amount + 1];
        dp[0] = 1;
        for (int coin : coins) {
            for (int i = coin; i <= amount; i++) {
                dp[i] += dp[i - coin];
            }
        }
        return dp[amount];
    }
}