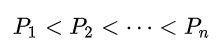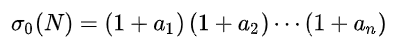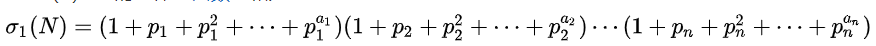质数的判定—试除法

时间复杂度：O(sqrt(n))
判断条件为 i <= n / i;
这种写法比根号n要快一点
同时注意也不能写成 i * i <= n; 当n接近于21亿时，i * i可能会溢出

1
2
3
4
5
6
7
boolean isPrime(int n) {
    if (n < 2) return false;
    for (int i = 2; i <= n / i; i++) {
        if (n % i == 0) return false;
    }
    return true;
}

分解质因数—试除法

苏教版小学五年级的数学知识，我连小学生都不如

算术基本定理,又称为正整数的唯一分解定理,即:每个大于1的自然数均可写为质数的积,而且这些素因子按大小排列之后,写法仅有一种方式。

例如84分解质因数为：$2^2 * 3 * 7$，即2出现了2次，3出现了1次，7出现了1次

1
2
3
4
5
6
7
8
9
10
11
12
static void divide(int n) {
    for (int i = 2; i <= n; i++) {
        if (n % i == 0) {
            int count = 0;
            while (n % i == 0) {
                count++;
                n /= i;
            }
            System.out.println(i + " " + count);
        }
    }
}

由于n中至多包含一个大于sqrt(n)的因子(反证法：如果存在两个大于sqrt(n)的因子，那他俩乘积必然大于n，故不成立)，所以我们可以把遍历范围设置成 2 - sqrt(n)，如果试除法除到最后的n，仍然大于1，则其就是最后一个因子

将O(n)的时间复杂度降低到 $O(logn)$ ~ $O(sqrt(n))$ 之间

1
2
3
4
5
6
7
8
9
10
11
12
13
static void divide(int n) {
    for (int i = 2; i <= Math.sqrt(n); i++) {
        if (n % i == 0) {
            int count = 0;
            while (n % i == 0) {
                count++;
                n /= i;
            }
            System.out.println(i + " " + count);
        }
    }
    if (n > 1) System.out.println(n + " " + 1);
}

筛质数

最普通的筛法 O(nlogn)

从2开始枚举每一个数，将每个数的倍数都筛掉

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class Main {
    static int N = 1000010;
    static int cnt;         //用来计数
    static int[] primes = new int[N];   //用来存放质数
    static boolean[] isPass = new boolean[N];   //用来判断当前数是否已经被pass掉了（不是质数）

    public static void main(String[] args) {
        getPrime(100);
        System.out.println(cnt);
        for (int i = 0; i < cnt; i++) {
            System.out.print(primes[i] + " ");
        }
    }

    static void getPrime(int n) {
        for (int i = 2; i <= n; i++) {
            if (isPass[i] == false)     //如果当前数没被pass掉，那它就是质数
                primes[cnt++] = i;      //将其存入数组中
            for (int j = i; j <= n; j += i) {   //将每一个数的倍数都pass掉，肯定不是质数
                isPass[j] = true;
            }
        }
    }
}

埃氏筛 O(nloglogn)

在上面的做法上进行一些优化，不用将每一个数的倍数都筛掉，只将每一个质数的倍数筛掉就可以了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class Main {
    static int N = 1000010;
    static int[] primes = new int[N];
    static int cnt;
    static boolean[] isPass = new boolean[N];

    public static void main(String[] args) {
        getPrime(100);
        System.out.println(cnt);
        for (int i = 0; i < cnt; i++) {
            System.out.print(primes[i] + " ");
        }
    }

    static void getPrime(int n) {
        for (int i = 2; i <= n; i++) {
            if (isPass[i] == false) {
                primes[cnt++] = i;
                for (int j = i; j <= n; j += i)
                    isPass[j] = true;
            }
        }
    }
}

约数

试除法求约数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import java.util.ArrayList;
import java.util.Collections;

public class Main {
    static ArrayList<Integer> list = new ArrayList<>();

    public static void main(String[] args) {
        getDivides(100);
        Collections.sort(list);
        for (int a : list) {
            System.out.print(a + " ");
        }
    }

    static void getDivides(int n) {
        for (int i = 1; i <= n / i; i++) {
            if (n % i == 0) {
                list.add(i);
                if (i != n / i) list.add(n / i);
            }
        }
    }
}

约数个数

任何一个大于1的自然数 ，如果N不为质数，都可以唯一分解成有限个质数的乘积

其中
且均为质数

定理应用
一个大于1的正整数N，如果它的标准分解式为: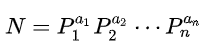

那么它的正因数个数为

它的全体正因数之和为

在分解质因数的时候，我们其实就已经求出了任意正整数N的标准分界式

1
2
3
4
5
6
7
8
9
10
11
12
13
static int getNumOfFactors(int n) {
    int res = 1;
    for (int i = 2; i <= n / i; i++) {
        int a = 0;
        while (n % i == 0) {
            n /= i;
            a++;
        }
        res *= (1 + a);     
    }
    if (n > 1) res *= 2;    //如果存在唯一一个大于sqrt(n)的因数，那么其上标只能为1，带入到公式也就是乘上(1 + 1) = 2
    return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
static void divide(int n) {
    for (int i = 2; i <= Math.sqrt(n); i++) {
        if (n % i == 0) {
            int count = 0;
            while (n % i == 0) {
                count++;
                n /= i;
            }
            System.out.println(i + " " + count);
        }
    }
    if (n > 1) System.out.println(n + " " + 1);
}

为了和下面的约数之和统一一下版本，写了个Hashmap版的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
static int getNumOfFactors(int x) {
    int res = 1;
    HashMap<Integer, Integer> map = new HashMap<>();
    for (int i = 2; i <= x / i; i++) {
        int count = 0;
        while (x % i == 0) {
            x /= i;
            count++;
        }
        map.put(i, count);
    }
    if (x > 1) map.put(x, 1);
    for (int c : map.values()) {
        res *= c + 1;
    }
    return res;
}

约数之和

直接套用公式就好了
基数为1，每次乘上p + 1，那么就会依次得到

p + 1

p^2 + p

p^3 + p^2 + p

···

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
static long getSumOfFactors(int x) {
    HashMap<Integer, Integer> map = new HashMap<>();
    for (int i = 2; i <= x / i; i++) {
        int count = 0;
        while (x % i == 0) {
            x /= i;
            count++;
        }
        map.put(i, count);
    }
    if (x > 1) map.put(x, 1);
    long res = 1;
    for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
        int p = entry.getKey(), count = entry.getValue();
        long tmp = 1;
        while (count-- > 0) tmp = p * tmp + 1;
        res *= tmp;
    }
    return res;
}

最大公约数

辗转相除法（欧几里得算法）

1
2
3
static int gcd(int a, int b) {
        return b == 0 ? a : gcd(b, a % b);
    }

最小公倍数公式 lcm = a * b / (gcd(a, b))