[NOI2001] 食物链

来源：洛谷
链接：https://www.luogu.com.cn/problem/P2024

题目描述

动物王国中有三类动物 A,B,C，这三类动物的食物链构成了有趣的环形。A 吃 B，B 吃 C，C 吃 A。

现有 N 个动物，以 1 － N 编号。每个动物都是 A,B,C 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 N 个动物所构成的食物链关系进行描述：

  • 第一种说法是 1 X Y，表示 X 和 Y 是同类。
  • 第二种说法是2 X Y，表示 X 吃 Y 。

此人对 N 个动物，用上述两种说法，一句接一句地说出 K 句话，这 K 句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

  • 当前的话与前面的某些真的话冲突，就是假话
  • 当前的话中 X 或 Y 比 N 大，就是假话
  • 当前的话表示 X 吃 X，就是假话

你的任务是根据给定的 N 和 K 句话，输出假话的总数。

输入格式

第一行两个整数，N，K，表示有 N 个动物，K 句话。

第二行开始每行一句话（按照题目要求，见样例）

输出格式

一行，一个整数，表示假话的总数。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5

样例输出 #1

1
3

提示

1 ≤ N ≤ 5 ∗ 10^4

1 ≤ K ≤ 10^5

分析

普通的并查集能维护连通性、传递性，通俗地说，亲戚的亲戚是亲戚。

然而当我们需要维护一些对立关系，比如 敌人的敌人是朋友 时，正常的并查集就很难满足我们的需求。

这时，种类并查集就诞生了。

常见的做法是将原并查集扩大一倍规模，并划分为两个种类。

在同个种类的并查集中合并，和原始的并查集没什么区别，仍然表达他们是朋友这个含义。

对于本题则需要扩容为3倍大小。

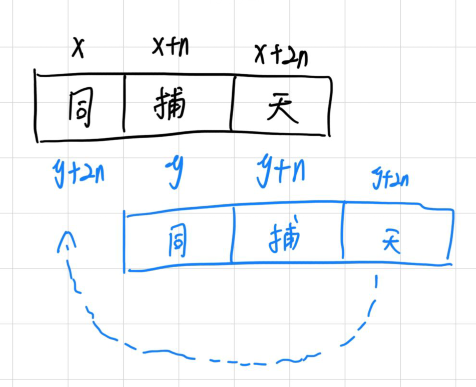
设我们有n个动物，那我们就开一个3n大小的并查集，1 - n存放A群系，n+1 - 2n存放B群系，2n+1 - 3n存放C群系

ABC之间的关系是A吃B、B吃C、C吃A，即B是A的猎物，C是A的天敌。

总结一下就是，对于每种生物，设x为其本身，那么x+n为其猎物，x+2n为其天敌

如果存在关系 1 x y ，则表明x和y是同类关系，那么y就不能是x的猎物或者天敌。

由刚刚我们得出的结论

设x为其本身，那么x+n为其猎物，x+2n为其天敌

如果y与x+n在同一集合，或者y与x+2n在同一集合，则说明这句是假话。

否则的话，将（x，y）放在同一集合，（x+n，y+n）放在同一集合，（x+2n，y+2n）放在同一集合。

对应的代码如下

1
2
3
4
5
6
7
8
9
if (z == 1) {
    if (find(x + n) == find(y) || find(x + 2 * n) == find(y)) {
        ans++;
        continue;
    }
    unity(x, y);
    unity(x + n, y + n);
    unity(x + 2 * n, y + 2 * n);
}

如果存在关系 2 x y，则表明x捕食y，那x和y就不能是同类关系，y也不能是x的天敌

由刚刚我们得出的结论

设x为其本身，那么x+n为其猎物，x+2n为其天敌

如果x与y在同一集合，或y与x+2n在同一集合，则说明这句话是假话

否则的话，将（y，x+n）放在同一集合，（y+n，x+2n）放在同一集合，（x，y+2n）放在同一集合。

献上丑图一张
对应的代码如下

1
2
3
4
5
6
7
8
9
if (z == 2) {
    if (find(x) == find(y) || find(x + 2 * n) == find(y)) {
        ans++;
        continue;
    }
    unity(x, y + 2 * n);
    unity(x + n, y);
    unity(x + 2 * n, y + n);
}

题目中还有两项特别的规定
当前的话中 X 或 Y 比 N 大，就是假话

1
2
3
4
if (x > n || y > n) {    
    ans++;
    continue;
}

当前的话表示 X 吃 X，就是假话

1
2
3
4
5
if(z == 2){
    if (x == y) {
        ans++;
        continue;
    }

到此为止就分析完毕了，下面是我们的完整代码

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
import java.util.Scanner;

public class Main {
    static int[] fa = new int[150005];
    static int n, k, ans;

    //查找祖宗+路径优化
    public static int find(int x) {
        return x == fa[x] ? x : (fa[x] = find(fa[x]));
    }

    //合并操作
    public static void unity(int x, int y) {
        int r1 = find(fa[x]), r2 = find(fa[y]);
        fa[r1] = r2;
    }

    public static void main(String[] args) {
        int x, y, z;
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        k = scan.nextInt();
        for (int i = 1; i <= 3 * n; ++i) fa[i] = i; //对于每种生物：设 x 为本身，x+n 为猎物，x+2*n 为天敌
        for (int i = 1; i <= k; ++i) {
            z = scan.nextInt();
            x = scan.nextInt();
            y = scan.nextInt();
            if (x > n || y > n) {
                ans++;
                continue;
            } // 不属于该食物链显然为假
            if (z == 1) {
                if (find(x + n) == find(y) || find(x + 2 * n) == find(y)) {
                    ans++;
                    continue;
                }
                //如果1是2的天敌或猎物，显然为谎言
                unity(x, y);
                unity(x + n, y + n);
                unity(x + 2 * n, y + 2 * n);
                //如果为真，那么1的同类和2的同类，1的猎物是2的猎物，1的天敌是2的天敌
            } else if (z == 2) {
                if (x == y) {
                    ans++;
                    continue;
                } //其实是废话但是可以稍微省点时间
                if (find(x) == find(y) || find(x + 2 * n) == find(y)) {
                    ans++;
                    continue;
                }
                //如果1是2的同类或猎物，显然为谎言
                unity(x, y + 2 * n);
                unity(x + n, y);
                unity(x + 2 * n, y + n);
                //如果为真，那么1的同类是2的天敌，1的猎物是2的同类，1的天敌是2的猎物
            }
        }
        System.out.println(ans);
    }
}

蓝桥侦探

来源：蓝桥云课
链接：https://www.lanqiao.cn/problems/1136/learning/

问题叙述

分析

本题只有两个种类，在大厅1和在大厅2，转换一下题意，在同一个大厅的是朋友，不在同一个大厅的是敌人

所以我们只需要创建2n大小的并查集就行。

1 - n表示朋友

n+1 - 2n表示敌军

给出的每一组数据都是告诉我们x与y是敌人，但敌人的敌人就是朋友

如果我们推导出x和y是朋友或者x和y都是敌军，那么就找到了内鬼

所以最终的判断条件如下

1
2
3
4
if (find(x) == find(y) || find(x + n) == find(y + n)) {
    res=x;
    break;
}

如果没找到内鬼，就将（x，y+n）合并。解释：y+n是y的敌人，x也是y的敌人，那x和y+n就是朋友。

同理，将（x+n，y）合并

Code

Java不用流加速会超时就很烦啊

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import java.io.*;

public class Main {
    static int[] f;
    
    public static int find(int x) {
        return x == f[x] ? x : (f[x] = find(f[x]));
    }

    public static void unity(int x, int y) {
        int r1 = find(f[x]), r2 = find(f[y]);
        f[r1] = r2;
    }

    public static void main(String[] args) throws IOException {
        StreamTokenizer sc = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
        int n, m, x, y,res=0;
        sc.nextToken();
        n = (int) sc.nval;
        sc.nextToken();
        m = (int) sc.nval;
        f = new int[2*n+1];
        for (int i = 1; i <= 2*n; i++) {
            f[i] = i;
        }
        while (m-- > 0) {
            sc.nextToken();
            x = (int) sc.nval;
            sc.nextToken();
            y = (int) sc.nval;
            if (find(x) == find(y) || find(x + n) == find(y + n)) {
                res=x;
                break;
            }
            unity(x, y + n);
            unity(x + n, y);
        }
        System.out.println(res);
    }
}