省份数量

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/bLyHh0

问题叙述

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

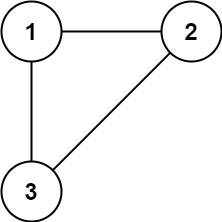
示例 1：

输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2：

输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

提示：
1 <= n <= 200
n == isConnected.length
n == isConnected[i].length
isConnected[i][j] 为 1 或 0
isConnected[i][i] == 1
isConnected[i][j] == isConnected[j][i]

分析

并查集的简单应用。

并查集是一种树型的数据结构，主要用于解决以下两个问题

  1. 将两个集合合并
  2. 询问两个元素是否在同一个集合当中

基本原理：每个集合用一棵树来表示。树根的编号就是整个集合的编号。每个节点存储它的父节点，parent[x]表示x的父节点。

对于每一个点，我们都存储一下它的父节点是谁，当我们相求某一个点属于哪个集合的时候，我们就求其父节点是谁，如果父节点不是树根，那么继续往上找，直到找到树根，因此我们可以用这种方式快速求出某个元素是属于哪个集合的。

问题1：如何判断树根？

  • if(parent[x] == x)

问题2：如何求x的集合编号？

  • while(parent[x] != x) x = parent[x];

问题3：如何合并两个集合？

  • 把一棵树，嫁接到另一棵树，成为另一棵树的儿子。p[x]是x的编号，p[y]是y的编号。p[x] = y;

根据题中的定义：省份是一组直接或间接相连的城市，组内不含其他没有相连的城市。
给我们的二维数组isConnected[i][j]表示：第i个城市和第j个城市相连。
我们用并查集，将所有的相连的城市合并，最终的祖宗节点个数，就是省份个数

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
    int cities;
    int[] parent;

    public int findCircleNum(int[][] isConnected) {
        cities = isConnected.length;
        parent = new int[cities];
        for (int i = 0; i < cities; i++) parent[i] = i;
        for (int i = 0; i < cities; i++) {
            for (int j = i + 1; j < cities; j++) {
                if (isConnected[i][j] == 1)
                    //如果i和j相连，那么将二者合并
                    union(i, j);
            }
        }
        int res = 0;
        for (int i = 0; i < cities; i++) {
            //最终有几个祖宗节点，那就是有几个省
            if (parent[i] == i)
                res++;
        }
        return res;
    }

    //合并
    public void union(int i, int j) {
        parent[find(i)] = find(j);
    }

    //找到祖宗节点+路径压缩 
    public int find(int index) {
        if (parent[index] != index) 
            parent[index] = find(parent[index]);
        return parent[index];
    }
}

冗余连接

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/redundant-connection

问题叙述

树可以看成是一个连通且 无环 的 无向 图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。

示例 1：

输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

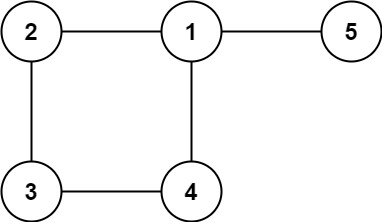
示例 2：

输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]
 
提示:

  • n == edges.length
  • 3 <= n <= 1000
  • edges[i].length == 2
  • 1 <= ai < bi <= edges.length
  • ai != bi
  • edges 中无重复元素
  • 给定的图是连通的

分析

通过并查集来寻找冗余的边。初始时，每个节点都属于不同的集合，遍历每一条边，判断这条边的两个顶点是否在同一个集合中。

  • 如果两个顶点不在一个集合中，说明加上这条边，不会出现环，那我们就直接把这两个集合合并
  • 如果两个顶点在一个集合中，那我们再加上这条边，必然会导致环的出现，为冗余的边，所以将当前边作为结果返回即可

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        int size = edges.length;
        int[] p = new int[size + 1];
        //初始化
        for (int i = 0; i < size; i++)
            p[i] = i;
        //x和y分别是当前边的两个祖宗
        for (int[] e : edges) {
            int x = find(p, e[0]);
            int y = find(p, e[1]);
            //如果祖宗不一样，那么直接合并
            if (x != y) p[x] = y;
            //否则当前边就是冗余边
            else return e;
        }
        return new int[0];
    }

    //找到祖宗节点+路径压缩
    public int find(int[] p, int x) {
        return x == p[x] ? x : (p[x] = find(p, p[x]));
    }
}

【模板】并查集

来源：洛谷
链接：https://www.luogu.com.cn/problem/P3367

题目描述

如题，现在有一个并查集，你需要完成合并和查询操作。

输入格式

第一行包含两个整数 $N,M$ ,表示共有 $N$ 个元素和 $M$ 个操作。

接下来 $M$ 行，每行包含三个整数 $Z_i,X_i,Y_i$ 。

当 $Z_i=1$ 时，将 $X_i$ 与 $Y_i$ 所在的集合合并。

当 $Z_i=2$ 时，输出 $X_i$ 与 $Y_i$ 是否在同一集合内，是的输出
Y ；否则输出 N 。

输出格式

对于每一个 $Z_i=2$ 的操作，都有一行输出，每行包含一个大写字母，为 Y 或者 N 。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4

样例输出 #1

1
2
3
4
N
Y
N
Y

提示

对于 $30%$ 的数据，$N \le 10$，$M \le 20$。

对于 $70%$ 的数据，$N \le 100$，$M \le 10^3$。

对于 $100%$ 的数据，$1\le N \le 10^4$，$1\le M \le 2\times 10^5$，$1 \le X_i, Y_i \le N$，$Z_i \in { 1, 2 }$。

分析

就当练练手了

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int N = scan.nextInt(), M = scan.nextInt();
        int[] p = new int[N + 1];
        for (int i = 0; i < p.length; i++) {
            p[i] = i;
        }
        while (M-- > 0) {
            int a = scan.nextInt();
            int b = scan.nextInt();
            int c = scan.nextInt();
            if (a == 2) {
                System.out.println(find(p, b) == find(p, c) ? "Y" : "N");
            } else union(p, b, c);
        }
    }

    public static void union(int[] p, int x, int y) {
        p[find(p, x)] = find(p, y);
    }

    public static int find(int[] p, int x) {
        return x == p[x] ? x : (p[x] = find(p, p[x]));
    }
}

亲戚

来源：洛谷
链接：https://www.luogu.com.cn/problem/P1551

题目背景

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。

题目描述

规定：$x$ 和 $y$ 是亲戚，$y$ 和 $z$ 是亲戚，那么 $x$ 和 $z$ 也是亲戚。如果 $x$，$y$ 是亲戚，那么 $x$ 的亲戚都是 $y$ 的亲戚，$y$ 的亲戚也都是 $x$ 的亲戚。

输入格式

第一行：三个整数 $n,m,p$，（$n,m,p \le 5000$），分别表示有 $n$ 个人，$m$ 个亲戚关系，询问 $p$ 对亲戚关系。

以下 $m$ 行：每行两个数 $M_i$，$M_j$，$1 \le M_i,~M_j\le N$，表示 $M_i$ 和 $M_j$ 具有亲戚关系。

接下来 $p$ 行：每行两个数 $P_i,P_j$，询问 $P_i$ 和 $P_j$ 是否具有亲戚关系。

输出格式

$p$ 行，每行一个 Yes 或 No。表示第 $i$ 个询问的答案为“具有”或“不具有”亲戚关系。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6

样例输出 #1

1
2
3
Yes
Yes
No

分析

依旧是一道练手题

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt(), m = scan.nextInt(), p = scan.nextInt();
        int[] parent = new int[n + 1];
        for (int i = 0; i < parent.length; i++) {
            parent[i] = i;
        }
        while (m-- > 0) {
            int a = scan.nextInt();
            int b = scan.nextInt();
            union(parent, a, b);
        }
        while (p-- > 0) {
            int x = scan.nextInt();
            int y = scan.nextInt();
            if (find(parent, x) == find(parent, y))
                System.out.println("Yes");
            else System.out.println("No");
        }
    }

    public static void union(int[] p, int x, int y) {
        p[find(p, x)] = find(p, y);
    }

    public static int find(int[] p, int x) {
        return x == p[x] ? x : (p[x] = find(p, p[x]));
    }
}