刷题日志--字典树Trie 6.2

更新日志

6.3

回来复盘一下，添加了"最大的异或"题解

6.2

初学前缀树

实现Trie（前缀树）

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/implement-trie-prefix-tree

问题叙述

Trie（发音类似 “try”）或者说前缀树是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

示例：
输入
[“Trie”, “insert”, “search”, “search”, “startsWith”, “insert”, “search”]
[[], [“apple”], [“apple”], [“app”], [“app”], [“app”], [“app”]]
输出
[null, null, true, false, true, null, true]

解释
Trie trie = new Trie();
trie.insert(“apple”);
trie.search(“apple”); // 返回 True
trie.search(“app”); // 返回 False
trie.startsWith(“app”); // 返回 True
trie.insert(“app”);
trie.search(“app”); // 返回 True

提示：
1 <= word.length, prefix.length <= 2000
word 和 prefix 仅由小写英文字母组成
insert、search 和 startsWith 调用次数总计不超过 3 * 10^4 次

分析

Trie又名字典树、前缀树、单词查找树等，可以理解成一棵26叉树，但它又与普通的树不同

先来看一下普通的二叉树的节点的属性，包含了节点值与孩子节点。

class TreeNode {
    int val;            //节点值
    TreeNode left;      //指向孩子节点
    TreeNode right;     //指向孩子节点
}

在来看一下Trie的定义，不难看出Trie节点中并没有保存字符值的变量，而是用字母映射表children，下标0-25分别对应着a-z

next数组中保存了对当前节点而言，下一个可能出现的所有字符的链接，因此可以通过一个父节点，预知它所有的子节点值。

class Trie {
    private Trie[] children;        //字母映射表
    private boolean isEnd;      //该节点是否为一个字符串的结束

    public Trie() {
        next = new Trie[26];
    }

    ···

}

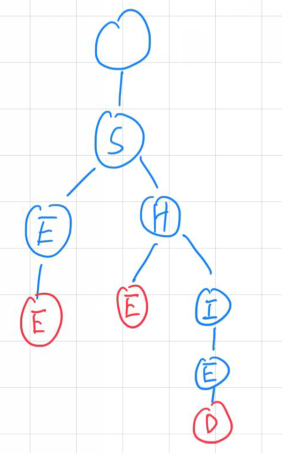
举个例子，包含三个单词"SEE", “SHIED”, "SHE"的Trie树会是什么样子

插入
描述：向Trie中插入一个单词
实现：首先先从根节点的子节点开始与word的第一个字符开始匹配，一直匹配到前缀链上没有对应的字符，那么此时就创建一个新节点，直到插入完word中的所有字符，同时将最后一个节点的isEnd设置为true，表示它是一个单词的结尾。
例如我们插入完"SHIED"后，要插入"SHE"，先拿"S"与根节点的子节点开始匹配，发现已经存在，不需要新建节点，继续匹配下一个字符"H"，也已经存在，继续匹配"E"字符，发现并不存在，此时我们新建一个节点（对应上图很容易理解）。

public void insert(String word) {
    Trie node = this;
    for (int i = 0; i < word.length(); i++) {
        int index = word.charAt(i) - 'a';
        if (node.children[index] == null)
            node.children[index] = new Trie();
        node = node.children[index];
    }
    node.isEnd = true;
}

查找
描述：查找 Trie 中是否存在单词 word
实现：从根结点的子结点开始，一直向下匹配即可，如果出现结点值为空就返回 false，如果匹配到了最后一个字符，那我们只需判断 node.isEnd即可。

public boolean search(String word) {
    Trie node = this;
    for (int i = 0; i < word.length(); i++) {
        int index = word.charAt(i) - 'a';
        if (node.children[index] == null) return false;
        node = node.children[index];
    }
    return node.isEnd;
}

前缀匹配
描述：判断 Trie 中是或有以 prefix 为前缀的单词
实现：比search还简单一点，也是从根节点的子节点开始，一直向下匹配，如果出现节点值为空，则返回fasle，如果匹配完所有字符都没有返回fasle，那就说明一定存在某个单词是以prefix为前缀的，结果返回true即可

public boolean startsWith(String prefix) {
    Trie node = this;
    for (int i = 0; i < prefix.length(); i++) {
        int index = prefix.charAt(i) - 'a';
        if (node.children[index] == null) return false;
        node = node.children[index];
    }
    return true;
}

Code

class Trie {
    private Trie[] children;
    private boolean isEnd;

    public Trie() {
        children = new Trie[26];
        isEnd = false;
    }

    public void insert(String word) {
        Trie node = this;
        for (int i = 0; i < word.length(); i++) {
            int index = word.charAt(i) - 'a';
            if (node.children[index] == null)
                node.children[index] = new Trie();
            node = node.children[index];
        }
        node.isEnd = true;
    }

    public boolean search(String word) {
        Trie node = this;
        for (int i = 0; i < word.length(); i++) {
            int index = word.charAt(i) - 'a';
            if (node.children[index] == null) return false;
            node = node.children[index];
        }
        return node.isEnd;
    }

    public boolean startsWith(String prefix) {
        Trie node = this;
        for (int i = 0; i < prefix.length(); i++) {
            int index = prefix.charAt(i) - 'a';
            if (node.children[index] == null) return false;
            node = node.children[index];
        }
        return true;
    }
}

单词频率

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/words-frequency-lcci

问题叙述

设计一个方法，找出任意指定单词在一本书中的出现频率。

你的实现应该支持如下操作：

WordsFrequency(book)构造函数，参数为字符串数组构成的一本书
get(word)查询指定单词在书中出现的频率

示例：
WordsFrequency wordsFrequency = new WordsFrequency({“i”, “have”, “an”, “apple”, “he”, “have”, “a”, “pen”});
wordsFrequency.get(“you”); //返回0，"you"没有出现过
wordsFrequency.get(“have”); //返回2，"have"出现2次
wordsFrequency.get(“an”); //返回1
wordsFrequency.get(“apple”); //返回1
wordsFrequency.get(“pen”); //返回1
提示：

book[i]中只包含小写字母
1 <= book.length <= 100000
1 <= book[i].length <= 10
get函数的调用次数不会超过100000

分析

上题使用isEnd来标识是否为一个字符串的结束，那这道题我们只需要把isEnd换成val即可，记录一下重复的单词个数。

Code

class Trie {
	private Trie[] children;
	private int val;

	public Trie() {
		children = new Trie[26];
		val = 0;
	}

	public void insert(String word) {
		Trie node = this;
		for (int i = 0; i < word.length(); i++) {
			int index = word.charAt(i) - 'a';
			if (node.children[index] == null)
				node.children[index] = new Trie();
			node = node.children[index];
		}
		node.val++;
	}

	public int search(String word) {
		Trie node = this;
		for (int i = 0; i < word.length(); i++) {
			int index = word.charAt(i) - 'a';
			if (node.children[index] == null) return 0;
			node = node.children[index];
		}
		return node.val;
	}
}

class WordsFrequency {
	Trie trie;

	public WordsFrequency(String[] book) {
		trie = new Trie();
		for (String s : book) {
			trie.insert(s);
		}
	}

	public int get(String word) {
		return trie.search(word);
	}
}

最大的异或

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/maximum-xor-of-two-numbers-in-an-array

问题叙述

给你一个整数数组 nums ，返回 nums[i] XOR nums[j] 的最大运算结果，其中 0 ≤ i ≤ j < n 。

进阶：你可以在 O(n) 的时间解决这个问题吗？

示例 1：
输入：nums = [3,10,5,25,2,8]
输出：28
解释：最大运算结果是 5 XOR 25 = 28.

示例 2：
输入：nums = [0]
输出：0

示例 3：
输入：nums = [2,4]
输出：6

示例 4：
输入：nums = [8,10,2]
输出：10

示例 5：
输入：nums = [14,70,53,83,49,91,36,80,92,51,66,70]
输出：127

提示：
1 <= nums.length <= 2 * 10^4
0 <= nums[i] <= 2^31 - 1

分析

前缀树与贪心的综合运用
要想得到一个最大的异或结果，假设nums[i]和nums[j]异或可以取得最大结果
异或运算的规则是：相同为0，不同为1.
题目的范围有31位2进制位，对于nums[i]而言，从其二进制的高位向低位开始运算，我们需要尽量保证每一位异或的结果为1，这样才能找到最大异或结果
所以我们先将所有的数存入Trie中，然后贪心的匹配每一位（优先考虑不同的二进制位）。例如1010110，我们要尽可能的匹配0101001

Code

class Trie {
	Trie[] ns;

	public Trie() {
		ns = new Trie[2];
	}

	public void insert(int x) {
		Trie trie = this;
		for (int i = 30; i >= 0; i--) {
			int u = x >> i & 1;
			if (trie.ns[u] == null)
				trie.ns[u] = new Trie();
			trie = trie.ns[u];
		}
	}

	public int search(int x) {
		int ans = 0;
		Trie trie = this;
		for (int i = 30; i >= 0; i--) {
			int a = x >> i & 1, b = 1 - a;
			if (trie.ns[b] != null) {
				ans += b << i;
				trie = trie.ns[b];
			} else {
				ans += a << i;
				trie = trie.ns[a];
			}
		}
		return ans;
	}
}

class Solution {
	public int findMaximumXOR(int[] xs) {
		Trie trie = new Trie();
		int res = 0;
		for (int n : xs) {
			trie.insert(n);
			int j = trie.search(n);
			res = Math.max(res, n ^ j);
		}
		return res;
	}
}