刷题日志--动态规划 5.9

比特位计数

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/counting-bits

问题叙述

给你一个整数 n ，对于 0 <= i <= n 中的每个 i ，计算其二进制表示中 1 的个数，返回一个长度为 n + 1 的数组 ans 作为答案。

示例 1：

输入：n = 2
输出：[0,1,1]
解释：
0 --> 0
1 --> 1
2 --> 10
示例 2：

输入：n = 5
输出：[0,1,1,2,1,2]
解释：
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101

提示：

0 <= n <= 105

进阶：

很容易就能实现时间复杂度为 O(n log n) 的解决方案，你可以在线性时间复杂度 O(n) 内用一趟扫描解决此问题吗？
你能不使用任何内置函数解决此问题吗？（如，C++ 中的 __builtin_popcount ）

分析

对于奇数：1的数量，比前面的偶数多一个，偶数以0结尾，奇数相较于它前面的偶数，把末尾的0变成了1
对于偶数：1的数量，跟偶数除以二的数字相同，相当于二进制右移了一位，抹掉一个0
所以奇数的状态转移方程为：dp[i] = dp[i - 1] +1;
偶数的状态转移方程为：dp[i] = dp[i / 2];

Code

class Solution {
    public int[] countBits(int n) {
        int[] dp = new int[n + 1];
        for (int i = 0; i <= n; i++)
            if (i % 2 == 1) dp[i] = dp[i - 1] + 1;
            else (i % 2 == 0) dp[i] = dp[i / 2];
        return dp;
    }
}

这是第一遍做的时候用的笨比方法,效率低下

class Solution {
    public int[] countBits(int n) {
        int[] res = new int[n + 1];
        for (int i = 0; i <= n; i++) {
            for (char c : Integer.toBinaryString(i).toCharArray()) {
                if(c == '1')
                    res[i]++;
            }
        }
        return res;
    }
}

粉刷房子

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/JEj789

问题叙述

假如有一排房子，共 n 个，每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种，你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。

当然，因为市场上不同颜色油漆的价格不同，所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个 n x 3 的正整数矩阵 costs 来表示的。

例如，costs[0][0] 表示第 0 号房子粉刷成红色的成本花费；costs[1][2] 表示第 1 号房子粉刷成绿色的花费，以此类推。

请计算出粉刷完所有房子最少的花费成本。

示例 1：
输入: costs = [[17,2,17],[16,16,5],[14,3,19]]
输出: 10
解释: 将 0 号房子粉刷成蓝色，1 号房子粉刷成绿色，2 号房子粉刷成蓝色。
最少花费: 2 + 5 + 3 = 10。

示例 2：
输入: costs = [[7,6,2]]
输出: 2

提示:

costs.length == n
costs[i].length == 3
1 <= n <= 100
1 <= costs[i][j] <= 20

分析

dp[i][0] 表示第i栋房子，粉刷成红色的最小花费
dp[i][1] 表示第i栋房子，粉刷成蓝色的最小花费
dp[i][2] 表示第i栋房子，粉刷成绿色的最小花费

又由于相邻的两栋房子不能刷成同一个颜色
故dp[i][0]的状态转移方程，只能从蓝色和绿色转移过来
那么dp[i][0]的最小花费，是蓝色或者绿色的最小花费的基础上，加上粉刷红色的花费
红色对应的状态转移方程为：dp[i][0] = Math.min(dp[i - 1][1] + costs[i][0], dp[i - 1][2] + costs[i][0]);
蓝色对应的状态转移方程为：dp[i][1] = Math.min(dp[i - 1][0] + costs[i][1], dp[i - 1][2] + costs[i][1]);
绿色对应的状态转移方程为：dp[i][2] = Math.min(dp[i - 1][0] + costs[i][2], dp[i - 1][1] + costs[i][2]);

Code

class Solution {
    public int minCost(int[][] costs) {
        int n = costs.length;
        int[][] dp = new int[n][3];
        dp[0][0] = costs[0][0];
        dp[0][1] = costs[0][1];
        dp[0][2] = costs[0][2];
        for (int i = 1; i < n; i++) {
            dp[i][0] = Math.min(dp[i - 1][1], dp[i - 1][2]) + costs[i][0];
            dp[i][1] = Math.min(dp[i - 1][0], dp[i - 1][2]) + costs[i][1];
            dp[i][2] = Math.min(dp[i - 1][0], dp[i - 1][1]) + costs[i][2];
        }
        return Math.min(dp[n - 1][0], Math.min(dp[n - 1][1], dp[n - 1][2]));
    }
}

其实不用开n * 3的dp数组，直接拿个临时变量存储就行

class Solution {
    public int minCost(int[][] costs) {
        int r = costs[0][0];
        int b = costs[0][1];
        int g = costs[0][2];
        for (int i = 1; i < costs.length; i++) {
            int red = r, blue = b, green = g;
            r = Math.min(blue, green) + costs[i][0];
            b = Math.min(red, green) + costs[i][1];
            g = Math.min(red, blue) + costs[i][2];
        }
        return Math.min(Math.min(r, b), g);
    }
}

下降路径最小和

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/minimum-falling-path-sum

问题叙述

给你一个 n x n 的方形整数数组 matrix ，请你找出并返回通过 matrix 的下降路径的最小和。

下降路径可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

示例 1：

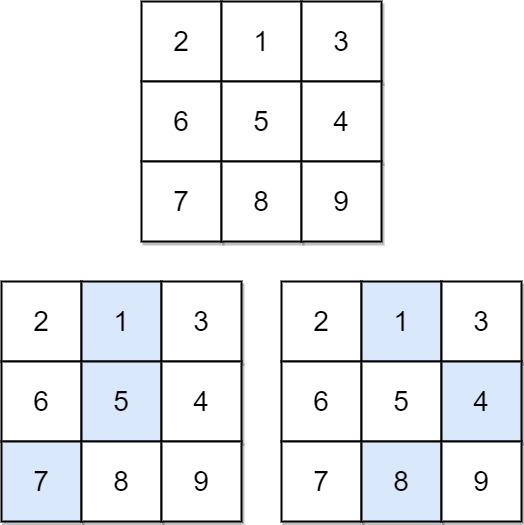
输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：如图所示，为和最小的两条下降路径

示例 2：

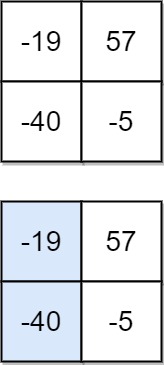
输入：matrix = [[-19,57],[-40,-5]]
输出：-59
解释：如图所示，为和最小的下降路径

提示：
n == matrix.length == matrix[i].length
1 <= n <= 100
-100 <= matrix[i][j] <= 100

分析

跟上题差不多，上题的状态转移只能由另外两个不同颜色的房子转移过来
本题的状态转移方程只能由本列和相邻的两列转移过来，要注意列的坐标有没有越界
状态转移方程为：Math.min(Math.min(matrix[i][j], matrix[i - 1][j - 1] + tmp), matrix[i - 1][j] + tmp);
由于我们需要判断一下是否列坐标是否越界，所以我们得拆开写

Code

这里就不新建一个dp数组了，可以直接在原数组上进行修改

class Solution {
    public int minFallingPathSum(int[][] matrix) {
        int n = matrix.length;
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < n; j++) {
                int tmp = matrix[i][j];
                matrix[i][j] = matrix[i - 1][j] + tmp;
                if (j - 1 >= 0) matrix[i][j] = Math.min(matrix[i][j], matrix[i - 1][j - 1] + tmp);
                if (j + 1 < n) matrix[i][j] = Math.min(matrix[i][j], matrix[i - 1][j + 1] + tmp);
            }
        }
        int min = Integer.MAX_VALUE;
        for (int i = 0; i < n; i++) {
            min = Math.min(min, matrix[n - 1][i]);
        }
        return min;
    }
}