岛屿数量
来源:力扣(Leetcode)
链接:https://leetcode.cn/problems/number-of-islands/
问题叙述
你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1
输入
grid = [
[“1”,”1”,”1”,”1”,”0”],
[“1”,”1”,”0”,”1”,”0”],
[“1”,”1”,”0”,”0”,”0”],
[“0”,”0”,”0”,”0”,”0”]
]
输出
1
示例 2
输入
grid = [
[“1”,”1”,”0”,”0”,”0”],
[“1”,”1”,”0”,”0”,”0”],
[“0”,”0”,”1”,”0”,”0”],
[“0”,”0”,”0”,”1”,”1”]
]
输出
3
提示
m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 ‘0’ 或 ‘1’
分析
DFS
遍历每一个格子,当遍历到一片陆地时(grud[x][y] == 1),res++,并从该陆地开始深度优先搜索,从该坐标(x, y)的四个方向(x+1, y), (x-1, y), (x, y+1), (x, y-1)做深度搜索。
终止条件:当x或y越界,或者grid[x][y] != 1,也就是碰到海洋时或碰到已遍历过的陆地。
同时我们也要标记一下已经遍历过的陆地,将已遍历过的格子设为2,避免以后重复搜索一片陆地。
最终岛屿的个数,也就是我们深度优先搜索的次数。
BFS
当然我们也可以使用BFS代替DFS
依旧是遍历每一个格子,如果当前格子为陆地,则将其加入到队列中,随后沿着该格子的四个方向进行广度优先搜索,将遍历到的每一个陆地格子标记为0,直到队列为空,搜索结束
最终岛屿的个数,也就是我们广度优先搜索的次数。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
int res = 0;
public int numIslands(char[][] grid) {
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == '1') {
res++;
dfs(grid, i, j);
}
}
}
return res;
}
void dfs(char[][] grid, int x, int y) {
if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length || grid[x][y] != '1') return;
grid[x][y] = '2';
dfs(grid, x - 1, y);
dfs(grid, x + 1, y);
dfs(grid, x, y + 1);
dfs(grid, x, y - 1);
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| class Solution {
public int numIslands(char[][] grid) {
int count = 0;
for (int i = 0; i < grid.length; i++)
for (int j = 0; j < grid[0].length; j++)
if (grid[i][j] == '1') {
bfs(grid, i, j);
count++;
}
return count;
}
void bfs(char[][] grid, int x, int y) {
LinkedList<int[]> deque = new LinkedList<>();
deque.add(new int[]{x, y});
while (!deque.isEmpty()) {
int[] ints = deque.pollFirst();
int i = ints[0];
int j = ints[1];
if (i - 1 >= 0 && grid[i - 1][j] == '1') {
deque.add(new int[]{i - 1, j});
grid[i - 1][j] = '0';
}
if (i + 1 < grid.length && grid[i + 1][j] == '1') {
deque.add(new int[]{i + 1, j});
grid[i + 1][j] = '0';
}
if (j - 1 >= 0 && grid[i][j - 1] == '1') {
deque.add(new int[]{i, j - 1});
grid[i][j - 1] = '0';
}
if (j + 1 < grid[0].length && grid[i][j + 1] == '1') {
deque.add(new int[]{i, j + 1});
grid[i][j + 1] = '0';
}
}
}
}
|
岛屿的周长
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/island-perimeter/
问题叙述
给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。
网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
示例 1

输入
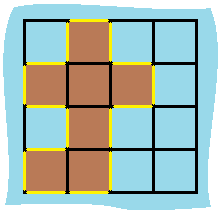
grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
输出
16
解释
它的周长是上面图片中的 16 个黄色的边
示例 2
输入
grid = [[1]]
输出
4
示例 3
输入
grid = [[1,0]]
输出
4
提示
row == grid.length
col == grid[i].length
1 <= row, col <= 100
grid[i][j] 为 0 或 1
分析
默认只有一片岛屿
当岛屿格子走向非岛屿格子时,周长+1。
非岛屿格子有两种,一种是走到界外,另一种是走到海洋。(玩过Minecraft的应该很好理解)
同时我们也需要将已经遍历过的岛屿格子设为2,避免兜圈子。
主循环遍历每一个格子,当我们遍历到岛屿格子时,就可以沿着四个方向深搜了。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Solution {
public int islandPerimeter(int[][] grid) {
for (int i = 0; i < grid.length; i++)
for (int j = 0; j < grid[0].length; j++)
if (grid[i][j] == 1)
return dfs(grid, i, j);
return 0;
}
int dfs(int[][] grid, int x, int y) {
if (x < 0 || y < 0 || x >= grid.length || y >= grid[0].length || grid[x][y] == 0) return 1;
if (grid[x][y] == 2) return 0;
grid[x][y] = 2;
return dfs(grid, x - 1, y) + dfs(grid, x + 1, y) + dfs(grid, x, y + 1) + dfs(grid, x, y - 1);
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| class Solution {
int res = 0;
int[] X = {-1, 0, 0, 1};
int[] Y = {0, -1, 1, 0};
public int islandPerimeter(int[][] grid) {
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == 1) {
bfs(grid, i, j);
}
}
}
return res;
}
void bfs(int[][] grid, int x, int y) {
LinkedList<int[]> deque = new LinkedList<>();
deque.add(new int[]{x, y});
grid[x][y] = 2;
while (!deque.isEmpty()) {
int[] tmp = deque.pollFirst();
int i = tmp[0];
int j = tmp[1];
for (int k = 0; k < 4; k++) {
int nx = i + X[k];
int ny = j + Y[k];
if (nx >= 0 && ny >= 0 && nx < grid.length && ny < grid[0].length && grid[nx][ny] == 1) {
grid[nx][ny] = 2;
deque.add(new int[]{nx, ny});
}
if (nx < 0 || ny < 0 || nx >= grid.length || ny >= grid[0].length || grid[nx][ny] != 1) {
if (nx < 0 || ny < 0 || nx >= grid.length || ny >= grid[0].length || grid[nx][ny] == 0)
res++;
continue;
}
}
}
}
}
|
岛屿的最大面积
来源:力扣(Leetcode)
链接:https://leetcode-cn.com/problems/max-area-of-island/
问题叙述
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
示例 1

输入
grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出
6
解释
答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。
示例 2
输入
grid = [[0,0,0,0,0,0,0,0]]
输出
0
提示
m == grid.length
n == grid[i].length
1 <= m, n <= 50
grid[i][j] 为 0 或 1
分析
依旧是遍历每一个格子,遍历到岛屿格子时,对该岛屿格子进行深搜,默认岛屿大小为1,沿四个方向深搜,已经遍历过的格子设为2。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| class Solution {
public int maxAreaOfIsland(int[][] grid) {
int res = 0;
for (int i = 0; i < grid.length; i++)
for (int j = 0; j < grid[0].length; j++)
if (grid[i][j] == 1)
res = Math.max(res, dfs(grid, i, j));
return res;
}
int dfs(int[][] grid, int x, int y) {
int tmp = 1;
if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length || grid[x][y] != 1) return 0;
grid[x][y] = 2;
tmp += dfs(grid, x - 1, y);
tmp += dfs(grid, x, y - 1);
tmp += dfs(grid, x + 1, y);
tmp += dfs(grid, x, y + 1);
return tmp;
}
}
class Solution {
public int maxAreaOfIsland(int[][] grid) {
int res = 0;
for (int i = 0; i < grid.length; i++)
for (int j = 0; j < grid[0].length; j++)
if (grid[i][j] == 1)
res = Math.max(res, dfs(grid, i, j));
return res;
}
int dfs(int[][] grid, int x, int y) {
if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length || grid[x][y] != 1) return 0;
grid[x][y] = 2;
return 1 + dfs(grid, x - 1, y) + dfs(grid, x, y - 1) + dfs(grid, x + 1, y) + dfs(grid, x, y + 1);
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| class Solution {
int res = 0;
int[] X = new int[]{-1, 0, 0, 1};
int[] Y = new int[]{0, -1, 1, 0};
public int maxAreaOfIsland(int[][] grid) {
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == 1)
res = Math.max(bfs(grid, i, j), res);
}
}
return res;
}
int bfs(int[][] grid, int x, int y) {
int size = 1;
LinkedList<int[]> deque = new LinkedList<>();
deque.add(new int[]{x, y});
grid[x][y] = 2;
while (!deque.isEmpty()) {
int[] tmp = deque.pollFirst();
int i = tmp[0];
int j = tmp[1];
for (int k = 0; k < 4; k++) {
int nx = i + X[k];
int ny = j + Y[k];
if (nx >= 0 && ny >= 0 && nx < grid.length && ny < grid[0].length && grid[nx][ny] == 1) {
deque.add(new int[]{nx, ny});
size++;
grid[nx][ny] = 2;
}
}
}
return size;
}
}
|