第十届蓝桥杯省赛 Java--B组

第十届蓝桥杯Java省赛B组题目下载 提取码: qx4j

试题 A: 组队(5分)

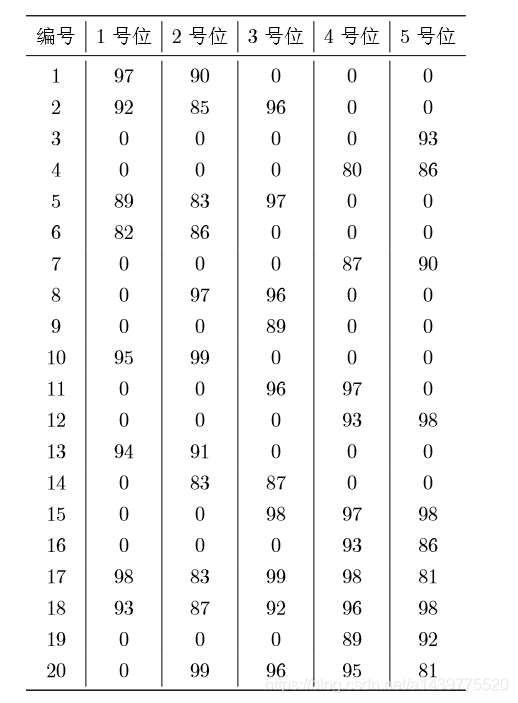
作为篮球队教练，你需要从以下名单中选出 1 号位至 5 号位各一名球员， 组成球队的首发阵容。 每位球员担任 1 号位至 5 号位时的评分如下表所示。请你计算首发阵容 1 号位至 5 号位的评分之和最大可能是多少？

思路分析

暴力枚举
要求这五个人不在同一行即可

代码

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int[][] arr = new int[20][5];
        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr[0].length; j++) {
                arr[i][j] = scan.nextInt();
            }
        }
        int max = -0x3f3f3f3f;
        for (int a = 0; a < 20; a++) {
            for (int b = 0; b < 20; b++) {
                for (int c = 0; c < 20; c++) {
                    for (int d = 0; d < 20; d++) {
                        for (int e = 0; e < 20; e++) {
                            int tmp = arr[a][0] + arr[b][1] + arr[c][2] + arr[d][3] + arr[e][4];
                            if ((a != b && a != c && a != d && a != e) && (b != c && b != d && b != e) && (c != d && c != e) && (d != e)) {
                                max = Math.max(tmp, max);
                            }
                        }
                    }
                }
            }
        }
        System.out.println(max);

    }
}

//测试用例

/*
97 90 0 0 0 92 85 96 0 0 0 0 0 0 93 0 0 0 80 86 89 83 97 0 0 82 86 0 0 0 0 0
0 87 90 0 97 96 0 0 0 0 89 0 0 95 99 0 0 0 0 0 96 97 0 0 0 0 93 98 94 91 0 0
0 0 83 87 0 0 0 0 98 97 98 0 0 0 93 86 98 83 99 98 81 93 87 92 96 98 0 0 0 89
92 0 99 96 95 81
*/

//答案：490

试题 B: 不同子串(5分)

一个字符串的非空子串是指字符串中长度至少为 1 的连续的一段字符组成 的串。例如，字符串aaab 有非空子串a, b, aa, ab, aaa, aab, aaab，一共 7 个。 注意在计算时，只算本质不同的串的个数。 请问，字符串0100110001010001 有多少个不同的非空子串？

思路分析

暴力枚举 set去重

代码

import java.util.HashSet;

public class Main {
    public static void main(String[] args) {
        String str = "0100110001010001";
        HashSet<String> set = new HashSet<>();
        for (int i = 0; i < str.length(); i++)
            for (int j = i; j < str.length(); j++)
                set.add(str.substring(i, j + 1));
        System.out.println(set.size());
    }
}


//答案：100

试题 C: 数列求值(10分)

给定数列 1, 1, 1, 3, 5, 9, 17, …，从第 4 项开始，每项都是前 3 项的和。求 第 20190324 项的最后 4 位数字。

思路分析

相当于三项的斐波那契数列
20190324项肯定会溢出
我们只保留末尾四位数字

代码

public class Main {
    public static void main(String[] args) {
        int[] dp = new int[20190324];
        dp[0] = dp[1] = dp[2] = 1;
        for (int i = 3; i < 20190324; i++)
            dp[i] = (dp[i - 1] + dp[i - 2] + dp[i - 3]) % 10000;
        System.out.println(dp[20190323]);
    }
}

//答案：4659

试题 D: 数的分解(10分)

本题总分：10 分

问题描述

把 2019 分解成 3 个各不相同的正整数之和，并且要求每个正整数都不包 含数字 2 和 4，一共有多少种不同的分解方法？ 注意交换 3 个整数的顺序被视为同一种方法，例如 1000+1001+18 和 1001+1000+18 被视为同一种。

思路分析

三个数凑成2019
有 ABC ACB BAC BCA CAB CBA 这六种
AAB ABA BAA 这三种
AAA 这一种
一共十种情况
题目要求3个各不相同的正整数
那我们就选取ABC这种情况 其中ABC是依次递增的

代码

public class Main {
    public static void main(String[] args) {
        int res = 0;
        for (int i = 1; i < 2019 / 3; i++) {
            if (method(i)) continue;
            for (int j = i + 1; j < 2019; j++) {
                if (method(j)) continue;
                int k = 2019 - i - j;
                if (method(k)) continue;
                if (k > j) res++;
            }
        }
        System.out.println(res);
    }

    static boolean method(int num) {
        return (num + "").contains("2") || (num + "").contains("4");
    }
}

//答案：40785

试题 E：迷宫(15分)

下图给出了一个迷宫的平面图，其中标记为 1 的为障碍，标记为 0 的为可以通行的地方。
010000
000100
001001
110000
迷宫的入口为左上角，出口为右下角，在迷宫中，只能从一个位置走到这个它的上、下、左、右四个方向之一。
对于上面的迷宫，从入口开始，可以按DRRURRDDDR 的顺序通过迷宫，一共 10 步。其中 D、U、L、R 分别表示向下、向上、向左、向右走。
对于下面这个更复杂的迷宫（30 行 50 列），请找出一种通过迷宫的方式，其使用的步数最少，在步数最少的前提下，请找出字典序最小的一个作为答案。
请注意在字典序中D<L<R<U。（如果你把以下文字复制到文本文件中，请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 maze.txt，内容与下面的文本相同）
01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000

思路分析

BFS

代码

import java.util.LinkedList;
import java.util.Scanner;

public class Main {
    static int n, m;
    static int[][] map = new int[100][100];
    static boolean[][] vis = new boolean[100][100];
    static int[] X = new int[]{1, 0, 0, -1};
    static int[] Y = new int[]{0, -1, 1, 0};//D,L,R,U
    static String[] stepPath = new String[]{"D", "L", "R", "U"};

    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        m = scan.nextInt();
        for (int i = 1; i <= n; i++) {
            String str = scan.next();
            for (int j = 1; j <= m; j++) {
                map[i][j] = str.charAt(j - 1);
            }
        }
        bfs();
    }

    public static void bfs() {
        LinkedList<Node> que = new LinkedList<>();
        que.offer(new Node(1, 1, ""));
        while (!que.isEmpty()) {
            Node tmp = que.poll();
            vis[tmp.x][tmp.y] = true;
            if (tmp.x == n && tmp.y == m) {
                System.out.println(tmp.path);
                return;
            }
            for (int i = 0; i < 4; i++) {
                int newX = tmp.x + X[i];
                int newY = tmp.y + Y[i];
                if (check(newX, newY)) {
                    Node node = new Node(newX, newY, tmp.path + stepPath[i]);
                    que.offer(node);
                }
            }
        }
    }

    private static boolean check(int x, int y) {
        if (x < 1 || x > n || y < 1 || y > m) return false;
        return !vis[x][y] && map[x][y] != '1';
    }

    static class Node {
        int x;
        int y;
        String path;

        public Node(int x, int y, String path) {
            this.x = x;
            this.y = y;
            this.path = path;
        }
    }
}
//答案：DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR

试题 F: 特别数的和(15分)

小明对数位中含有 2、0、1、9 的数字很感兴趣（不包括前导 0），在 1 到 40 中这样的数包括 1、2、9、10 至 32、39 和 40，共 28 个，他们的和是 574。 请问，在 1 到 n 中，所有这样的数的和是多少？

输入格式

输入一行包含两个整数 n。

输出格式

输出一行，包含一个整数，表示满足条件的数的和。

样例输入

40

样例输出

574

评测用例规模与约定

对于 20% 的评测用例，1≤n≤10。
对于 50% 的评测用例，1≤n≤100。
对于 80% 的评测用例，1≤n≤1000。
对于所有评测用例，1≤n≤10000。

思路分析

送分题

代码

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        int sum = 0;
        for (int i = 1; i <= n; i++) {
            if ((i + "").contains("2") || (i + "").contains("0") || (i + "").contains("1") || (i + "").contains("9"))
                sum += i;
        }
        System.out.println(sum);
    }
}

试题 G: 外卖店优先级(20分)

“饱了么”外卖系统中维护着 N 家外卖店，编号 1 ∼ N。每家外卖店都有 一个优先级，初始时 (0 时刻) 优先级都为 0。 每经过 1 个时间单位，如果外卖店没有订单，则优先级会减少 1，最低减 到 0；而如果外卖店有订单，则优先级不减反加，每有一单优先级加 2。 如果某家外卖店某时刻优先级大于 5，则会被系统加入优先缓存中；如果 优先级小于等于 3，则会被清除出优先缓存。 给定 T 时刻以内的 M 条订单信息，请你计算 T 时刻时有多少外卖店在优 先缓存中。

输入格式

第一行包含 3 个整数 N、M 和 T。 以下 M 行每行包含两个整数 ts 和 id，表示 ts 时刻编号 id 的外卖店收到 一个订单。

输出格式

输出一个整数代表答案。

样例输入

2 6 6
1 1
5 2
3 1
6 2
2 1
6 2

样例输出

1

样例解释

6 时刻时，1 号店优先级降到 3，被移除出优先缓存；2 号店优先级升到 6， 加入优先缓存。所以是有 1 家店 (2 号) 在优先缓存中。

评测用例规模与约定

对于 80% 的评测用例，1≤ N,M,T ≤10000。
对于所有评测用例，1≤ N,M,T ≤100000，1 ≤ ts ≤ T，1 ≤ id ≤ N。

思路分析

DP
创建一个二维数组dp
dp[i][j]初始化为在 i时刻 j店铺 拥有的订单数
拿样例输入距离就是 dp[1][1]表示在1时刻 1店铺有一个订单 我们直接dp[ts][id]++即可(允许同一时刻收到多个订单 优先级与订单数成正比)
当前时刻的优先级只与上一时刻的优先级有关
如果当前店铺当前时刻有订单(dp[i][j]>0) 那么当前店铺当前时刻的优先级 就是 当前店铺上一时刻的优先级的基础上 + 2 *（当前店铺当前时刻订单数）
否则当前店铺的优先级-1 也就是在上一时刻的优先级的基础上-1 此时我们需要判断一下上一时刻优先级是否为0
每次变更完优先级之后 判断是否加入或删除于优先缓存中
内存超限 通过90%的样例
优化思路：HashMap(以后再写)

代码

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int N = scan.nextInt(), M = scan.nextInt(), T = scan.nextInt();
        int[][] dp = new int[T + 1][N + 1];
        boolean[] isPriority = new boolean[N + 1];
        for (int i = 0; i < M; i++)
            dp[scan.nextInt()][scan.nextInt()]++;
        for (int i = 1; i <= T; i++)
            for (int j = 1; j <= N; j++)
                if (dp[i][j] > 0) {
                    dp[i][j] = dp[i - 1][j] + dp[i][j] * 2;
                    if (dp[i][j] > 5)
                        isPriority[j] = true;
                } else {
                    dp[i][j] = dp[i - 1][j] == 0 ? 0 : dp[i - 1][j] - 1;
                    if (dp[i][j] <= 3)
                        isPriority[j] = false;
                }
        int res = 0;
        for (boolean a : isPriority)
            if (a) res++;
        System.out.println(res);
    }
}

试题 H: 人物相关性分析(20分)

小明正在分析一本小说中的人物相关性。他想知道在小说中 Alice 和 Bob 有多少次同时出现。 更准确的说，小明定义 Alice 和 Bob“同时出现”的意思是：在小说文本 中 Alice 和 Bob 之间不超过 K 个字符。 例如以下文本： ThisisastoryaboutAliceandBob.AlicewantstosendaprivatemessagetoBob. 假设 K = 20，则 Alice 和 Bob 同时出现了 2 次，分别是”Alice and Bob” 和”Bob. Alice”。前者 Alice 和 Bob 之间有 5 个字符，后者有 2 个字符。 注意: 1. Alice 和 Bob 是大小写敏感的，alice 或 bob 等并不计算在内。 2. Alice 和 Bob 应为单独的单词，前后可以有标点符号和空格，但是不能 有字母。例如 Bobbi 並不算出现了 Bob。

输入格式

第一行包含一个整数 K。 第二行包含一行字符串，只包含大小写字母、标点符号和空格。长度不超过 1000000。

输出格式

输出一个整数，表示 Alice 和 Bob 同时出现的次数。

样例输入

20
This is a story about Alice and Bob.Alice wants to send a private message to Bob.

样例输出

2

评测用例规模与约定

对于所有评测用例，1≤ K ≤1000000。

思路分析

分别创建两个一维数组Alice和Bob 用来存储Alice和Bob在文章中出现的位置
需要判断Alice和Bob前后的字符不为字母
Alice[i]表示 第i个Alice出现的位置是Alice[i]
我们只需要判断在 (Alice[i]-K-3,Alice[i]+5+K)这个区间内出现了多少个Bob即可
使用双指针
依次遍历Bob的索引值
Left指针记录上述区间内的第一个Bob的索引值Bob[left]
Right指针记录上述区间内的最后一个Bob的索引值Bob[right]
然后我们用right-left就是当前区间内的Bob数

代码

import java.util.Scanner;

public class Main {
    public static long result = 0;
    public static int K;
    public static String text;
    public static int length;

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        K = in.nextInt();
        in.nextLine();
        text = in.nextLine();
        length = text.length();
        int[] Alice = new int[1000000];
        int[] Bob = new int[1000000];
        int count1 = 0, count2 = 0;
        for (int x = 0; x < length; x++) {
            if (!IsLetter(x - 1) && !IsLetter(x + 5) && text.startsWith("Alice", x))
                Alice[count1++] = x;
            if (!IsLetter(x - 1) && !IsLetter(x + 3) && text.startsWith("Bob", x))
                Bob[count2++] = x;
        }
        if (count1 == 0 || count2 == 0)
            result = 0;
        else {
            int left = 0, right = 0;
            for (int x = 0; x < count1; x++) {
                while (right < count2 && Bob[right] <= Alice[x] + K + 5)
                    right++;
                while (Bob[left] + 3 + K < Alice[x])
                    left++;
                result += right - left;
            }
        }
        System.out.println(result);
    }

    public static boolean IsLetter(int index) {
        if (index < 0 || index >= length)
            return false;
        char charAt = text.charAt(index);
        return (charAt >= 'a' && charAt <= 'z') || (charAt >= 'A' && charAt <= 'Z');
    }
}

试题 I: 后缀表达式(25分)

给定 N 个加号、M 个减号以及 N + M + 1 个整数 A1,A2,··· ,AN+M+1，小 明想知道在所有由这 N 个加号、M 个减号以及 N + M +1 个整数凑出的合法的 后缀表达式中，结果最大的是哪一个？
请你输出这个最大的结果。 例如使用1 2 3 + -，则 “2 3 + 1 -” 这个后缀表达式结果是 4，是最大的。

输入格式

第一行包含两个整数 N 和 M。 第二行包含 N + M + 1 个整数 A1,A2,··· ,AN+M+1。

输出格式

输出一个整数，代表答案。

样例输入

1 1 1 2 3

样例输出

4

评测用例规模与约定

对于所有评测用例，0≤ N,M ≤100000，−10^9 ≤ Ai ≤10^9。

思路分析

分类讨论

1. 没有负号
   没有负号就直接把所有数加起来 就是结果
2. 有负号
   只要有一个负号 就能把所有的负数变成正数

• 如果数字都是正数 那就用这些正数之和 减去一个最小的正数 --> 最大数-最小数+剩余正数之和
• 如果数字都是负数 那就用最大的负数 减去剩余所有负数之和 --> 最大数-最小数-剩余负数之和=最大数-最小数+剩余数的绝对值
• 如果有正有负 最大的整数-最小的负数+剩余数的绝对值之和(一个负号可以把所有数变成正数 减去负数等于加上正数)
  总结一下就是 排序之后，最大数-最小数 然后和其他数的绝对值全部相加。

代码

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int[] arr = new int[n + m + 1];
        for (int i = 0; i < n + m + 1; i++)
            arr[i] = sc.nextInt();
        long res = 0;
        if (m == 0) {
            for (int i : arr)
                res += i;
        } else {
            Arrays.sort(arr);
            int ans = arr[arr.length - 1] - arr[0];
            for (int i = 1; i < n + m; i++)
                if (arr[i] >= 0) res += arr[i];
                else res -= arr[i];
            res += ans;
        }
        System.out.println(res);
    }
}

试题 J：灵能传输(25分)

题目背景

在游戏《星际争霸 II》中，高阶圣堂武士作为星灵的重要 AOE 单位，在 游戏的中后期发挥着重要的作用，其技能”灵能风暴“可以消耗大量的灵能对 一片区域内的敌军造成毁灭性的伤害。经常用于对抗人类的生化部队和虫族的 刺蛇飞龙等低血量单位。

问题描述

你控制着 n 名高阶圣堂武士，方便起见标为 1,2,··· ,n。每名高阶圣堂武士 需要一定的灵能来战斗，每个人有一个灵能值 ai 表示其拥有的灵能的多少（ai 非负表示这名高阶圣堂武士比在最佳状态下多余了 ai 点灵能，ai 为负则表示这 名高阶圣堂武士还需要 −ai 点灵能才能到达最佳战斗状态）。现在系统赋予了 你的高阶圣堂武士一个能力，传递灵能，每次你可以选择一个 i ∈ [2,n−1]，若 ai ≥ 0 则其两旁的高阶圣堂武士，也就是 i−1、i + 1 这两名高阶圣堂武士会从 i 这名高阶圣堂武士这里各抽取 ai 点灵能；若 ai < 0 则其两旁的高阶圣堂武士， 也就是 i−1,i+1 这两名高阶圣堂武士会给 i 这名高阶圣堂武士 −ai 点灵能。形 式化来讲就是 ai−1+ = ai,ai+1+ = ai,ai−= 2ai。

灵能是非常高效的作战工具，同时也非常危险且不稳定，一位高阶圣堂 武士拥有的灵能过多或者过少都不好，定义一组高阶圣堂武士的不稳定度为 maxn i=1|ai|，请你通过不限次数的传递灵能操作使得你控制的这一组高阶圣堂武 士的不稳定度最小。

输入格式

本题包含多组询问。输入的第一行包含一个正整数 T 表示询问组数。 接下来依次输入每一组询问。 每组询问的第一行包含一个正整数 n，表示高阶圣堂武士的数量。 接下来一行包含 n 个数 a1,a2,··· ,an。

输出格式

输出 T 行。每行一个整数依次表示每组询问的答案。

样例输入

3
3
5 -2 3
4
0 0 0 0
3
1 2 3

样例输出

3
0
3

样例说明

对于第一组询问：
对 2 号高阶圣堂武士进行传输操作后 a1 = 3，a2 = 2，a3 = 1。答案为 3。
对于第二组询问：
这一组高阶圣堂武士拥有的灵能都正好可以让他们达到最佳战斗状态。

样例输入

3
4
-1 -2 -3 7
4
2 3 4 -8
5
-1 -1 6 -1 -1

样例输出

5
7
4

样例输入

见文件trans3.in。

样例输出

见文件trans3.ans。

数据规模与约定

对于所有评测用例，T ≤3，3≤n≤300000，|ai|≤10^9。
评测时将使用 25 个评测用例测试你的程序，每个评测用例的限制如下：

注意：本题输入量较大请使用快速的读入方式。